Cho đa thức P(x)= x2017 - 18x2016 + 11x2015 + 6x + 1. Với a0 là số nguyên bất kỳ khác 0 cho trước, xác định dãy (an) như sau: an+1 =P(an). Chứng minh rằng với mọi cặp số nguyên dương m, n phân biệt thì am , an nguyên tố cùng nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Với số tự nhiên n ≥ 1, ta có:
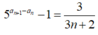
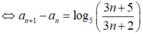
![]()
Suy ra:
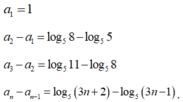
Cộng tương ứng hai vế các đẳng thức trên ta có ![]() với mọi số tự nhiên n
≥
1
với mọi số tự nhiên n
≥
1
Để ![]()
![]()
Ta kiểm tra với các giá trị k ∈ ℕ từ bé đến lớn
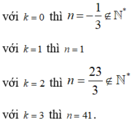
Vậy số nguyên n > 1 nhỏ nhất là n = 41( ứng với k = 3).

đề thấy hơi chán,từ số kia =2an,mẫu số cx chia hết cho 2 thì sao tối giản đc hả bạn ơi

Đề thi tin học trẻ BT phải ko b?
Mà bài này giải sao nhỉ?
Muốn xem code để tham khảo quá!!!
sắp xếp lại các phần tử theo chiều tăng dần rồi đặt kết quả muốn tìm = 1, so sánh nó với từng phần tử trong mảng, nếu bé hơn thì dừng chương trình và đó là kết quả, nếu không thỉ cộng kết quả cho phần tử đang được so sánh.
code :
program giai;uses crt;var n,m,i,c,t : integer;A : array[1..100] of integer;beginclrscr;write('so phan tu cua day so :');readln(m);for i:=1 to m do begin readln(A[i]); end;for i:= 1 to m do for n:=i+1 to m do if A[i] > A[n] then begin c:= A[i]; A[i] := A[n]; A[n] := c; end;t:= 1;for i:=1 to m-1 do if t < A[i] then break else t:= t+ A[i];writeln(t);readln;end.