Cho hình chữ nhật ABCD có AB= a\(\sqrt{2}\), AD= a. Gọi M là trung điểm của CD.
a) CMR MB ⊥ AC
b) Tính sinMAC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
Nguyễn Minh Quang
Giáo viên
11 tháng 12 2020
ta có diện tích ADM \(=\frac{AD.AM}{2}=\frac{AD.AB}{4}=\frac{a.b}{4}\)
diện tích DMN \(=\frac{AD.NM}{2}=\frac{AD.MB}{4}=\frac{AD.AB}{8}=\frac{a.b}{8}\)
27 tháng 10 2021
a: Xét ΔHAB có
N là trung điểm của HB
M là trung điểm của HA
Do đó: NM là đường trung bình của ΔAHB
Suy ra: \(NM=\dfrac{AB}{2}=2\left(cm\right)\)
23 tháng 8 2015
Theo định lý Ta-let \(\frac{IA}{IC}=\frac{IM}{ID}=\frac{AM}{CD}=\frac{1}{2}\to IA=\frac{1}{2}IC,ID=2IM\to IA=\frac{1}{3}AC,ID=\frac{2}{3}DM.\)
Mà theo định lý Pitago:
\(AC^2=AD^2+DC^2=3a^2,MD^2=\left(\frac{a}{2}\right)^2+\left(a\sqrt{2}\right)^2=\frac{9a^2}{4}\to AC=a\sqrt{3},MD=\frac{3a}{2}\)
Vậy ta có \(IA=\frac{1}{3}\cdot a\sqrt{3}=\frac{a\sqrt{3}}{3},ID=\frac{2}{3}\cdot\frac{3a}{2}=a\to IA+ID=\frac{a\sqrt{3}}{3}+a=\frac{\left(3+\sqrt{3}\right)a}{3}.\)
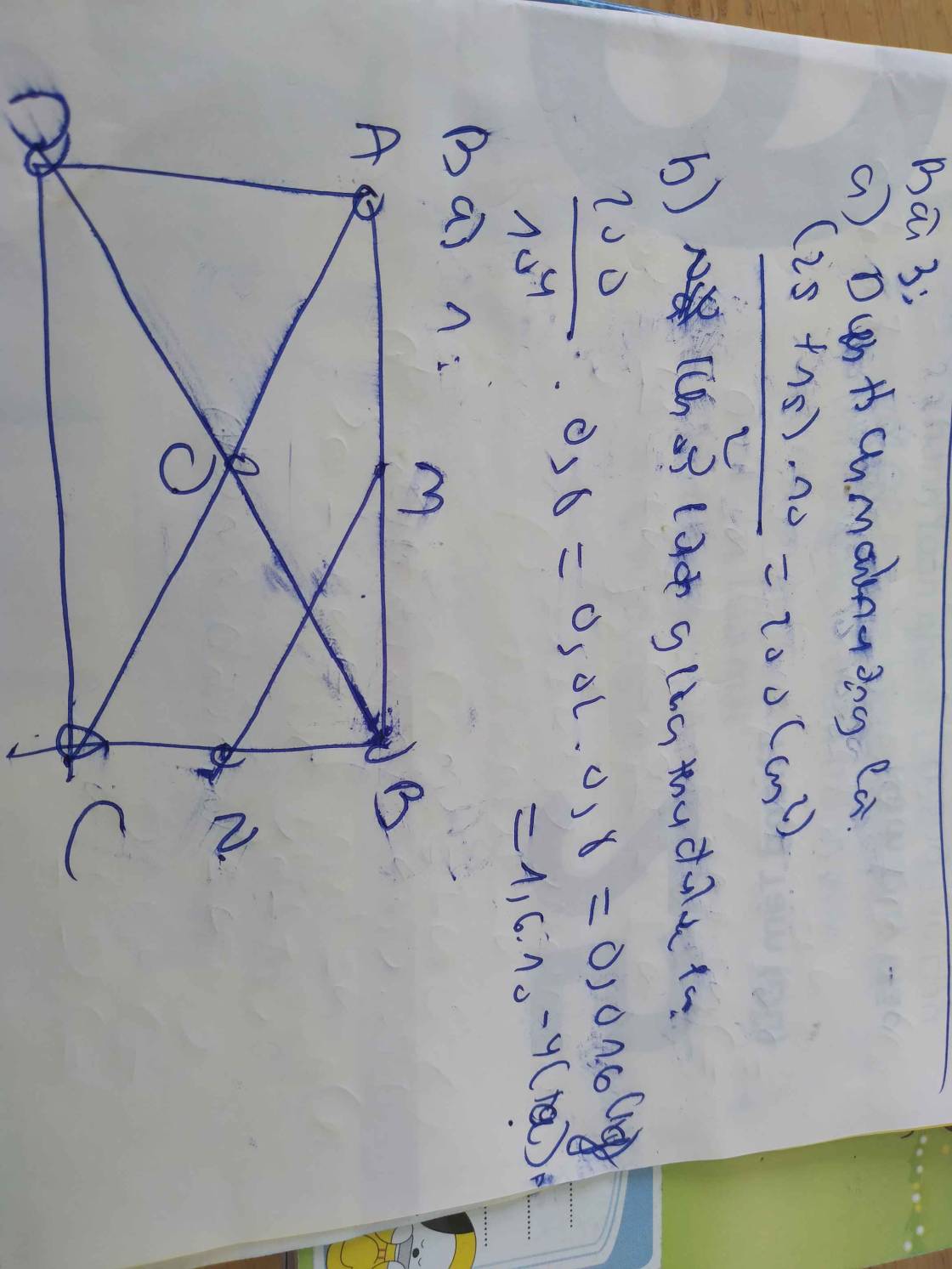
a: Xét ΔCBM vuông tại C và ΔBAC vuông tại B có
CB/BA=CM/BC
=>ΔCBM đồng dạng với ΔBAC
=>góc CBM=góc BAC
=>góc CBM+góc ACB=90 độ
=>MB vuông góc AC
b: \(MC=\dfrac{a\sqrt{2}}{2}\)
\(AM=\sqrt{AD^2+DM^2}=\dfrac{\sqrt{6}}{2}a\)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{3}\)
\(cosMAC=\dfrac{AM^2+AC^2-MC^2}{2\cdot AM\cdot AC}=\dfrac{2\sqrt{2}}{3}\)
=>sin MAC=1/3