\(\sqrt{x^2-6x+9}+x=11\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 9 2023
a: =>|2x-1|=3
=>2x-1=3 hoặc 2x-1=-3
=>2x=-2 hoặc 2x=4
=>x=2 hoặc x=-1
c: \(\Leftrightarrow\left|x-3\right|=11-x\)
=>x<=11 và (x-3)^2=(11-x)^2
=>x<=11 và x^2-6x+9=x^2-22x+121
=>x<=11 và 16x=112
=>x=7
d:
ĐKXĐ: 3x+19>=0
=>x>=-19/3
PT =>x>=-3 và (3x+19)=(x+3)^2=x^2+6x+9
=>x>=-3 và x^2+6x+9-3x-19=0
=>x>=-3 và (x+5)(x-2)=0
=>x=2
e: =>\(\sqrt{x^2+x+5}=x+1\)
=>x>=-1 và x^2+x+5=x^2+2x+1
=>x>=-1 và 2x+1=x+5
=>x=4
Y
2 tháng 7 2023
Câu b bạn có bị lỗi dấu căn không mà sao nó kéo dài cả 2 vế pt vậy :v
\(a,\sqrt{x^2-6x+9}+x=11\\ \Leftrightarrow\sqrt{\left(x-3\right)^2}=11-x\)
\(\Leftrightarrow\left|x-3\right|=11-x\\ TH_1:x\ge3\\ x-3=11-x\\ \Leftrightarrow2x=14\\ \Leftrightarrow x=7\left(tm\right)\)
\(TH_2:x< 3\\ -x+3=11-x\\ \Leftrightarrow-x+x=11-3\\ \Leftrightarrow0=8\left(VL\right)\)
Vậy \(S=\left\{7\right\}\)
\(c,\sqrt{16\left(x+1\right)}-\sqrt{9\left(x+1\right)}=4\) \(\left(dk:x\ge-1\right)\)
\(\Leftrightarrow\sqrt{4^2}.\sqrt{\left(x+1\right)}-\sqrt{3^2}.\sqrt{\left(x+1\right)}=4\left(1\right)\)
Đặt \(a=\sqrt{x+1}\left(a\ge0\right)\)
Pt trở thành : \(4a-3a=4\Leftrightarrow a=4\left(tmdk\right)\)
\(\Rightarrow\sqrt{x+1}=4\\ \Rightarrow\left(\sqrt{x+1}\right)^2=16\\ \Rightarrow\left|x+1\right|=16\)
\(TH_1:x\ge-1\\ x+1=16\Leftrightarrow x=15\left(tm\right)\\ TH_2:x< -1\\ -x-1=16\Leftrightarrow x=-17\left(tm\right)\)
Nhưng loại TH2 vì dk ban đầu là \(x\ge-1\)
Vậy \(S=\left\{15\right\}\)
\(d,\sqrt{9x+9}+\sqrt{4x+4}=\sqrt{x+1}\left(dk:x\ge-1\right)\\ \Leftrightarrow\sqrt{9}.\sqrt{x+1}+\sqrt{4}.\sqrt{x+1}-\sqrt{x+1}=0\)
Đặt \(\sqrt{x+1}=a\left(a\ge0\right)\)
Tới đây bạn làm tương tự câu c nha.
T
23 tháng 7 2019
d) Bài này có thể dùng hằng đẳng thức rồi phá dấu GTTĐ nhưng theo em là khá mất công nên bình phương lên rồi quy về pt bậc 2 cho lẹ:)
PT \(\Leftrightarrow4x^2-4x+1=x^2-6x+9\)
\(\Leftrightarrow3x^2+2x-8=0\Leftrightarrow\left[{}\begin{matrix}x=\frac{4}{3}\\x=-2\end{matrix}\right.\) (delta là ra:D)
Vậy..
31 tháng 8 2021
c: Ta có: \(\sqrt{x^2}=x\)
\(\Leftrightarrow\left|x\right|=x\)
hay \(x\ge0\)
d: Ta có: \(\sqrt{x^2-2x+1}=x-1\)
\(\Leftrightarrow\left|x-1\right|=x-1\)
hay \(x\ge1\)
28 tháng 7 2020
Ta có: \(11-\sqrt{x^2-6x+9}=\sqrt{25}\)
\(\Leftrightarrow11-\left|x-3\right|=5\)
\(\Leftrightarrow\left|x-3\right|=6\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=6\\x-3=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=9\\x=-3\end{matrix}\right.\)
Vậy: S={-3;9}
23 tháng 7 2019
a) \(\sqrt{x^2-6x+9}+x=11\)
\(\Rightarrow\sqrt{\left(x-3\right)^2}+x=11\)
\(\Rightarrow x-3+x=11\)
\(\Rightarrow2x=14\Rightarrow x=7\)
Vậy........
b) \(\sqrt{3x^2-4x+3}=1-2x\)
\(3x^2-4x+3=1-4x+4x^2\)
\(3x^2-4x^2-4x+4x=-2\)
\(-x^2=-2\)
\(2=x^2\Rightarrow\orbr{\begin{cases}x=\sqrt{2}\\x=-\sqrt{2}\end{cases}}\)
Vậy.........
23 tháng 7 2019
d) \(\sqrt{4x^2-4x+1}=\sqrt{x^2-6x+9}\)
\(\Rightarrow2x-1=x-3\)
\(\Rightarrow x=1-3\)
\(\Rightarrow x=-2\)
Vậy x=-2
9 tháng 7 2021
f) Ta có: \(\sqrt{16\left(x+1\right)}-\sqrt{9\left(x+1\right)}=4\)
\(\Leftrightarrow4\left|x+1\right|-3\left|x+1\right|=4\)
\(\Leftrightarrow\left|x+1\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=4\\x+1=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\)
g) Ta có: \(\sqrt{9x+9}+\sqrt{4x+4}=\sqrt{x+1}\)
\(\Leftrightarrow5\sqrt{x+1}-\sqrt{x+1}=0\)
\(\Leftrightarrow x+1=0\)
hay x=-1
25 tháng 7 2016
a) pt<=> \(\sqrt{\left(x-2\right)^2}+\sqrt{\left(x-3\right)^2}=1\)
<=>\(\left|x-2\right|+\left|x-3\right|=1\)
đến đây chia 3 trường hợp để phá trị tuyệt đối là ra
b) \(\sqrt{\left(\sqrt{x+2}-2\right)^2}+\sqrt{\left(\sqrt{x+2}-3\right)^2}=1\)
<=> \(\left|\sqrt{x+2}-2\right|+\left|\sqrt{x+2}-3\right|=1\)
câu này cũng tương tự câu a nha
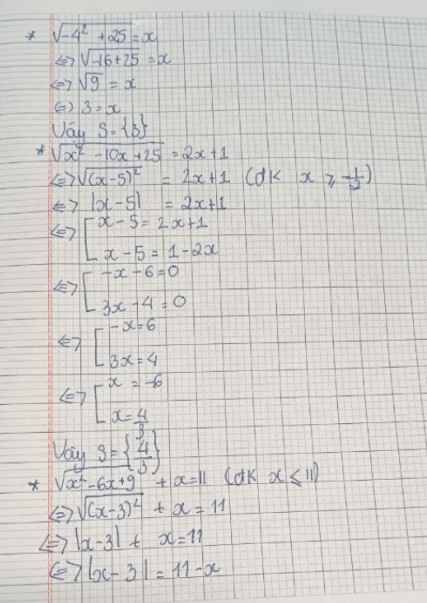
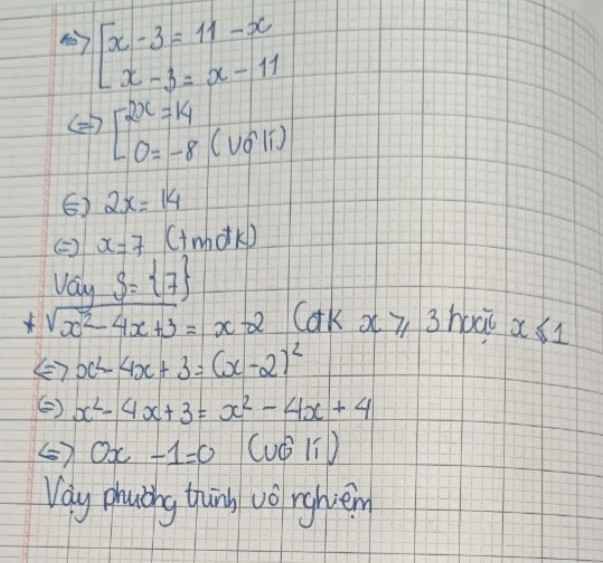
\(\sqrt{x^2-6x+9}+x=11\); (ĐKXĐ\(\forall x\in R\))
<=> \(\sqrt{x^2-6x+9}=11-x\)
<=> \(\sqrt{\left(x-3\right)^2}=11-x\)
<=> \(|x-3|=11-x\)
<=> \(\left[{}\begin{matrix}x-3=11-x\\x-3=-11+x\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}2x=14\\0x=-8\left(vô\right)lí\left(\right)\end{matrix}\right.\)
<=> x=7 (thỏa mãn ĐKXĐ)
Vậy phương trình có nghiệm là x=7