Có bao nhiêu số nguyên n thỏa mãn điều kiện sau:
a. n2 - 3n2 - 36 = 0
b. n2 - 3n2 -36 < 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow3< =n^2< =36\)
mà n là số nguyên
nên \(n^2\in\left\{4;9;16;25;36\right\}\)
hay \(n\in\left\{2;-2;3;-3;4;-4;5;-5;6;-6\right\}\)
Vậy: Có 10 số nguyên n thỏa mãn bài toán

a: \(n^3-2⋮n-2\)
=>\(n^3-8+6⋮n-2\)
=>\(6⋮n-2\)
=>\(n-2\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
=>\(n\in\left\{3;1;4;0;5;-1;8;-4\right\}\)
b: \(n^3-3n^2-3n-1⋮n^2+n+1\)
=>\(n^3+n^2+n-4n^2-4n-4+3⋮n^2+n+1\)
=>\(3⋮n^2+n+1\)
=>\(n^2+n+1\in\left\{1;-1;3;-3\right\}\)
mà \(n^2+n+1=\left(n+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}\forall n\)
nên \(n^2+n+1\in\left\{1;3\right\}\)
=>\(\left[{}\begin{matrix}n^2+n+1=1\\n^2+n+1=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}n^2+n=0\\n^2+n-2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}n\left(n+1\right)=0\\\left(n+2\right)\left(n-1\right)=0\end{matrix}\right.\Leftrightarrow n\in\left\{0;-1;-2;1\right\}\)

Chia cả tử và mẫu của phân thức cho n 3 ( n 3 là lũy thừa bậc cao nhất của n trong phân thức), ta được:
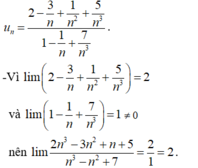
Chọn C.

Đáp án C
Chia cả tử và mẫu của phân thức cho n3 ( n3 là lũy thừa bậc cao nhất củan trong phân thức), ta được:
u n = 2 n 3 - 3 n 2 + n + 5 n 3 - n 2 + 7 = 2 - 3 n + 1 n 2 + 5 n 3 1 - 1 n + 7 n 3 .
Vì l i m 2 - 3 n + 1 n 2 + 5 n 3 = 2 và l i m 1 - 1 n + 7 n 3 = 1 ≢ 0 nên l i m 2 n 3 - 3 n 2 + n + 5 n 3 - n 2 + 7 = 2 1 = 2 .
Sao khó vậy nè !
mk ko có bít !
a)\(n^2-3n^2-36=0\Leftrightarrow-2n^2-36=0\Leftrightarrow-2n^2=36\Leftrightarrow n^2=-18\)
mà \(n^2\ge0\forall n\)=> không có số nguyên nào thỏa mãn\(n^2-3n^2-36=0\)
a)\(n^2-3n^2-36< 0\Leftrightarrow-2n^2-36< 0\Leftrightarrow-2n^2< 36\Leftrightarrow n^2>-18\)
=>Vậy \(n^2-3n^2-36< 0\) với mọi số tự nhiên n