Các bạn giúp mình làm ý d với ạ! Mình xin cảm ơn các bạnTừ điểm M nằm ngoài đường tròn vẽ tiếp tuyến MA tới đường tròn (O; R), ( A là tiếp điểm). Gọi E là trung điểm đoạn AM và hai điểm I, H lần lượt là hình chiếu của E và A trên đường thẳng OM. Qua M vẽ cát tuyến MBC tới đường tròn (O) sao cho MB < MC và tia MC nằm giữa hai tia MA, MO.a) Chứng minh các hệ thức: MA2 = MB.MC; MA2 =...
Đọc tiếp
Các bạn giúp mình làm ý d với ạ! Mình xin cảm ơn các bạn
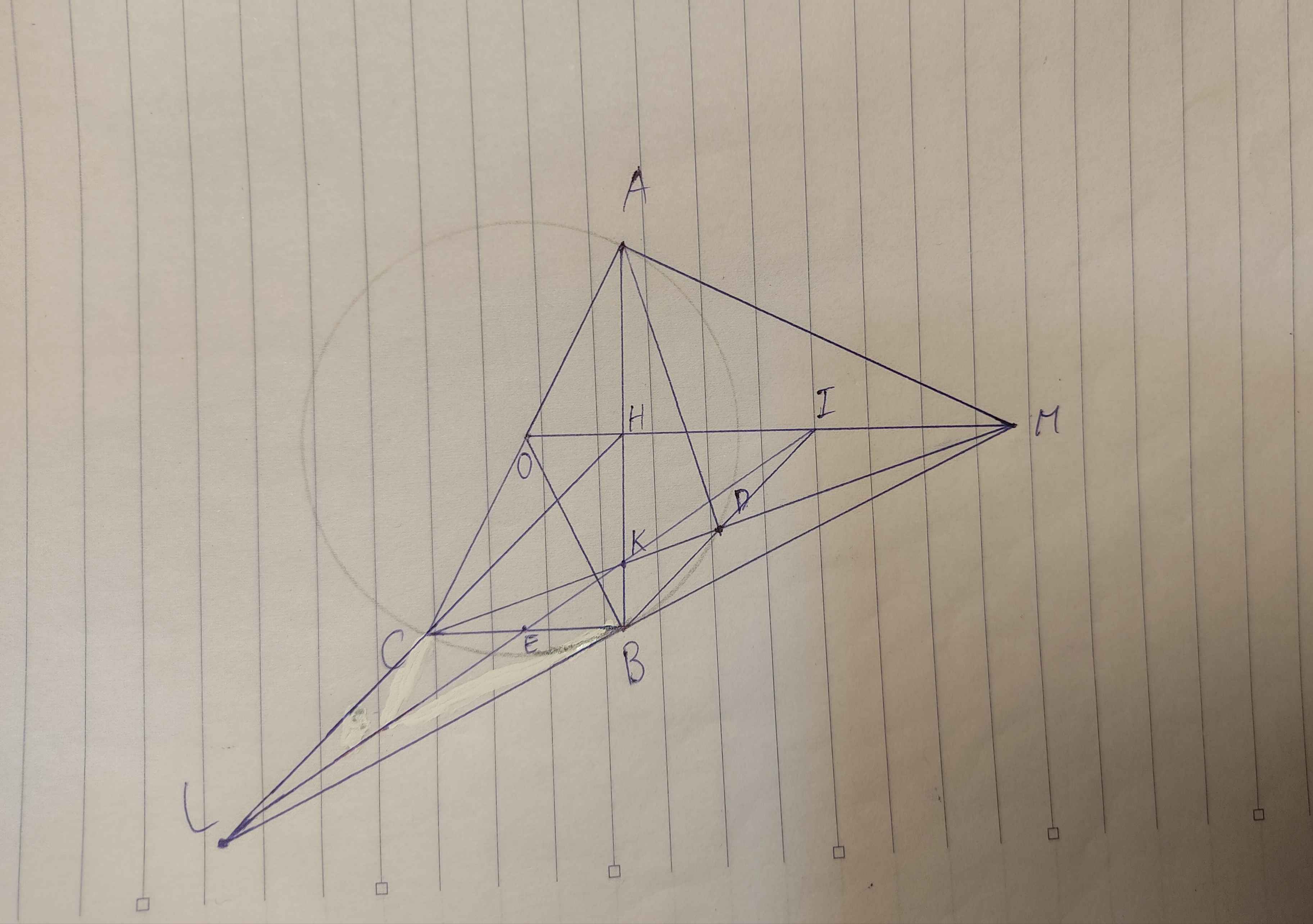
Từ điểm M nằm ngoài đường tròn vẽ tiếp tuyến MA tới đường tròn (O; R), ( A là tiếp điểm). Gọi E là trung điểm đoạn AM và hai điểm I, H lần lượt là hình chiếu của E và A trên đường thẳng OM. Qua M vẽ cát tuyến MBC tới đường tròn (O) sao cho MB < MC và tia MC nằm giữa hai tia MA, MO.
a) Chứng minh các hệ thức: MA2 = MB.MC; MA2 = MH.MO.
b) Chứng minh ∆MBH đồng dạng ∆MOC. Từ đó chứng minh tứ giác BCOH nội tiếp đường tròn.
c) Chứng minh . Vẽ tiếp tuyến IK tới đường tròn (O) với K là tiếp điểm. và ∆MKH vuông tại K.
d) Giả sử BC = 3BM và D là trung điểm đoạn MC. Chứng minh: MC tiếp xúc với đường tròn ngoại tiếp ∆ODH
ý c làm thế nào vậy bạn?
a) Xét đường tròn (O) có tiếp tuyến MA, cát tuyến MBC => MA2 = MB.MC (Hệ thức lượng đường tròn) (đpcm)
Xét \(\Delta\)MOA vuông tại A, đường cao AH => MA2 = MH.MO (Hệ thức lượng tam giác vuông) (đpcm)
b) Từ câu a ta có: MB.MC = MH.MO (=AM2) => \(\Delta\)MBH ~ \(\Delta\)MOC (c.g.c) => ^MHB = ^MCO
=> Tứ giác BCOH nội tiếp đường tròn (đpcm).
c) Áp dụng ĐL Pytagore, ta có các đẳng thức về cạnh:
IK2 = OI2 - OK2 = OI2 - OA2 = (OM - IM)2 - OA2 = OM2 - 2.OM.IM + IM2 - OA2 = AM2 - MH.MO + IM2
= AM2 - AM2 + IM2 = IM2 => IK = IM. Do đó: IK = IM = IH = MH/2
Xét \(\Delta\)MKH có: Trung tuyến KI=MH/2 (cmt) => \(\Delta\)KMH vuông tại K (đpcm).
d) Từ câu a: \(MA^2=MB.MC=\frac{MC}{4}.MC=\frac{MC^2}{4}\) => MA = MC/2 = MD
Từ đó: MA2 = MD2 = MH.MO => \(\Delta\)MDH ~ \(\Delta\)MOD (c.g.c) => ^MDH = ^MOD = 1/2.Sđ(HD(ODH)
Suy ra: MC tiếp xúc với đường tròn (ODH) (đpcm).