Cíu mik vớii ạ :< Rút gọn biểu thức: D=(3/4xy+3y)(x-12y)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 3 2023
a: \(M=\dfrac{x^2+2x+1-x^2-3}{2\left(x-1\right)\left(x+1\right)}=\dfrac{2\left(x-1\right)}{2\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x+1}\)
b: x thuộc {0;0,5}
=>x=0 hoặc x=0,5
Khi x=0 thì M=1/0+1=1
Khi x=0,5 thì M=1/0,5+1=1/1,5=2/3
=>M min=2/3 và M max=1
HN
4 tháng 7 2018
\(2x\left(x-3y\right)-4y\left(x+2\right)-2\left(x^2-3y-4xy\right)\)
\(=2x^2-6xy-4xy+8y-2x^2-6y-8xy\)
\(=2x^2-10xy+8y-2x^2-14xy\)
\(=10xy+8y-14xy\)
\(=-4xy+8y\)
\(=-4.\left(\frac{-2}{3}.\frac{3}{4}\right)+8.\frac{3}{4}\)
\(=-4.\frac{-1}{2}+6\)
\(=2+6=8\)
YT
4 tháng 7 2018
\(2x^2-6xy-4xy-8y-2x^2+6y+8xy\)
\(=-2y-2xy\)
thay \(x=\frac{-2}{3};y=\frac{3}{4}\) vào biểu thức ta có
\(-2.\frac{3}{4}-2.\frac{-2}{3}\frac{3}{4}=\frac{-3}{2}+1=\frac{-3+2}{2}=\frac{-1}{2}\)
nếu có sai bn thông cảm
12 tháng 5 2018
* Rút gọn:
\(A=\left(x^2+xy-y^2\right)-x^2-4xy-3y^2\)
\(A=x^2+xy-y^2-x^2-4xy-3y^2\)
\(A=\left(x^2-x^2\right)+\left(xy-4xy\right)+\left(-y^2-3y^2\right)\)
\(A=-3xy-4y^2\)
* Tính:
Thay x=0,5 và y= -4 vào biểu thức trên, ta được:
\(-3.0,5.\left(-4\right)=-1,5.\left(-4\right)=6\)
Vậy: giá trị biểu thức \(A=-3xy-4y^2\)tại x=0,5 và y=-4 là 8
MN
1
18 tháng 12 2023
Bài 1:
a: Sửa đề \(x^3y-2x^2y+xy\)
\(=y\left(x^3-2x^2+x\right)\)
\(=x\cdot y\cdot\left(x^2-2x+1\right)\)
\(=xy\left(x-1\right)^2\)
b: Sửa đề: \(x^2-9-2xy+y^2\)
\(=\left(x^2-2xy+y^2\right)-9\)
\(=\left(x-y\right)^2-9\)
\(=\left(x-y-3\right)\left(x-y+3\right)\)
Bài 2:
a: ĐKXĐ: \(x\notin\left\{3;-3;-1\right\}\)
b: \(A=\left(\dfrac{x}{x+3}-\dfrac{2}{x-3}+\dfrac{x^2-1}{9-x^2}\right):\left(2-\dfrac{x+5}{x+3}\right)\)
\(=\left(\dfrac{x}{x+3}-\dfrac{2}{x-3}-\dfrac{x^2-1}{\left(x-3\right)\left(x+3\right)}\right):\dfrac{2x+6-x-5}{x+3}\)
\(=\dfrac{x\left(x-3\right)-2\left(x+3\right)-x^2+1}{\left(x+3\right)\left(x-3\right)}\cdot\dfrac{x+3}{x+1}\)
\(=\dfrac{x^2-3x-2x-6-x^2+1}{x-3}\cdot\dfrac{1}{x+1}\)
\(=\dfrac{-5x-5}{\left(x-3\right)\left(x+1\right)}=-\dfrac{5\left(x+1\right)}{\left(x-3\right)\left(x+1\right)}=-\dfrac{5}{x-3}\)
c: \(x^2-x-2=0\)
=>\(\left(x-2\right)\left(x+1\right)=0\)
=>\(\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(nhận\right)\\x=-1\left(loại\right)\end{matrix}\right.\)
Thay x=2 vào A, ta được:
\(A=\dfrac{-5}{2-3}=\dfrac{-5}{-1}=5\)
HN
4 tháng 7 2018
\(2x\left(x-3y\right)-4y\left(x+2\right)-2\left(x^2-3y-4xy\right)\)
\(=2x^2-3y-4xy+8y-2x^2+3y+4xy\)
\(=-2y-2xy\)
Thay x,y ta có:
\(-2y-2xy=-2\left(\frac{3}{4}\right)-2\left(\frac{-2}{3}.\frac{3}{4}\right)\)
\(-2y-2xy=\frac{-3}{2}-2.\frac{-1}{2}\)
\(-2y-2xy=\frac{-3}{2}-\left(-1\right)\)
\(-2y-2xy=\frac{-3}{2}+1=\frac{-3}{2}+\frac{2}{2}=\frac{-1}{2}\)
Vậy biểu thức trên có giá trị bằng \(\frac{-1}{2}\)
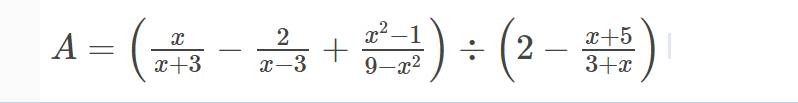
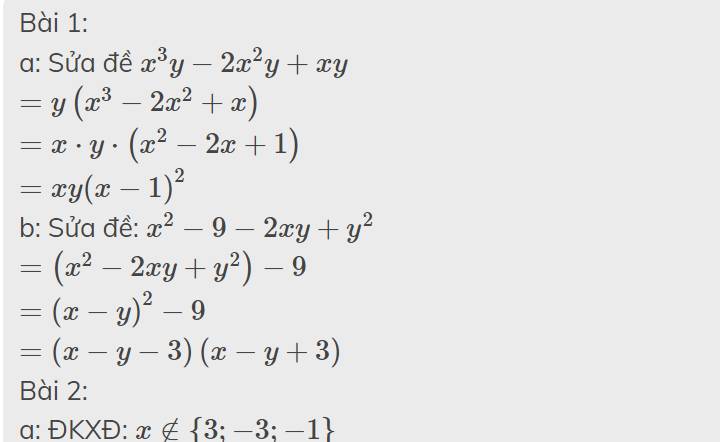
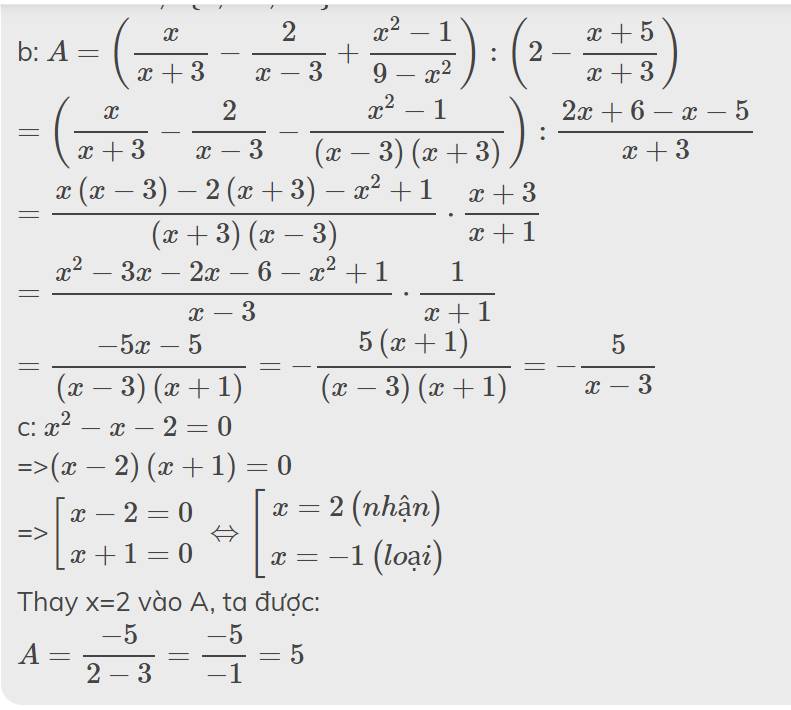
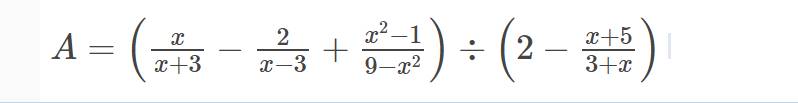
\(D=\left(\dfrac{3}{4}xy+3y\right)\left(x-12y\right)\\ =x\left(\dfrac{3}{4}xy+3y\right)-12y\left(\dfrac{3}{4}xy+3y\right)\\ =\dfrac{3}{4}x^2y+3xy-9xy^2-36y^2\)
Cảm ơn ạ