Help me plsssss
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
P
1
30 tháng 10 2021
Refer:
123 Cau Giay Rd, Hanoi
Nov 20, 2020
Hello Anna,
How are you doing? Are you interested in an art exhibition? Let’s join an Exhibition of Modern at Arts Centre with me this weekend. It is held at 9 o’clock this Saturday morning. I think we will meet at 8.15 at the bus stop near the Arts Center and then we’ll go to the exhibition together.
Write to me soon. I’m sure it will be fun.
Love,
Linh
LT
1
3 tháng 12 2021
Ngồi buồn nhớ mẹ ta xưa
Miếng nhai cơm búng , lưỡi lừa cá xương
Bé thì nhờ mẹ , nhờ cha
Lớn lên nhờ vợ lúc già nhờ con
Lên non với biết non cao
Nuôi con mới biết công lao mẹ , thầy
Ơn cha nặng lắm ai ơi
Nghĩa mẹ bằng trời , chín tháng cưu mang
Con người có tổ , có tông
Như cây có cuội , như sông có nguồn
k mik nha !
22 tháng 7 2023
=>\(25\cdot\dfrac{\sqrt{a-3}}{5}-7\cdot\dfrac{2}{3}\cdot\sqrt{a-3}-7\sqrt{a^2-9}+18\cdot\dfrac{1}{3}\sqrt{a^2-9}=0\)
=>\(\sqrt{a-3}\cdot\dfrac{1}{3}-\sqrt{a^2-9}=0\)
=>\(\sqrt{a-3}\left(\dfrac{1}{3}-\sqrt{a+3}\right)=0\)
=>a-3=0 hoặc a+3=1/9
=>a=3 hoặc a=-26/9
CN
1
14 tháng 6 2020
\(\frac{119}{153}=\frac{7}{9}\)
\(\frac{322}{345}=\frac{14}{15}\)
Học tốt
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2021
\(P=sin^22x-\left[2sin\dfrac{x}{2}cos\dfrac{x}{2}\left(cos^4\dfrac{x}{2}-sin^4\dfrac{x}{2}\right)\right]^2\)
\(=sin^22x-\left[sinx\left(cos^2\dfrac{x}{2}-sin^2\dfrac{x}{2}\right)\left(cos^2\dfrac{x}{2}+sin^2\dfrac{x}{2}\right)\right]^2\)
\(=sin^22x-\left[sinx.cosx.1\right]^2\)
\(=sin^22x-\left[\dfrac{1}{2}sin2x\right]^2\)
\(=\dfrac{3}{4}sin^22x=\dfrac{3}{4}\left(1-cos^22x\right)=\dfrac{3}{4}\left(1-\dfrac{1}{4}\right)=\dfrac{9}{16}\)
15 tháng 10 2023
`#3107.101107`
c)
Ta có:
`2x = 3y`
`=> x/3 = y/2 => x/15 = y/10`
`4y = 5z`
`=> y/5 = z/4 => y/10 = z/8`
`=> x/15 = y/10 = z/8`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/15 = y/10 = z/8 = (x - y - z)/(15 - 10 - 8) = (-27)/(-3) = 27/3 = 9`
`=> x/15 = y/10 = z/8 = 9`
`=>`\(x=15\cdot9=135\\ y=9\cdot10=90\\ z=8\cdot9=72\)
Vậy, giá trị của `x; y; z` lần lượt là `135; 90; 72`
d)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(x - 5)/3 = (y - 4)/2 = (x - 5 + y - 4)/(3 + 2) = (x + y - 5 - 4)/5 = (-1-9)/5 = (-10)/5 = -2`
`=> (x - 5)/3 = (y - 4)/2 = -2`
`=>`
\(x=\left(-2\cdot3\right)+5=-1\)
\(y=\left(-2\cdot2\right)+4=0\)
Vậy, giá trị của `x; y` lần lượt là `-1; 0`
e)
`(x - 1)/2 = (y - 2)/3 = (z - 3)/4`
`=> (x - 1)/2 = (2y - 4)/6 = (3z - 9)/12`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(x - 1)/2 = (2y - 4)/6 = (3z - 9)/12 = (x - 1 - (2y - 4) + 3z - 9)/(2 - 6 + 12) =`\(\dfrac{x-1-2y+4+3z-9}{8}=\dfrac{x-2y+3z+\left(-1+4-9\right)}{8}\\ =\dfrac{-10-6}{8}=\dfrac{-16}{8}=-2\)
`=> (x - 1)/2 = (y - 2)/3 = (z - 3)/4 = -2`
`=>`\(x=\left(-2\cdot2\right)+1=-3\); \(y=\left(-2\cdot3\right)+2=-4\); \(z=\left(-2\cdot4\right)+3=-5\)
Vậy, giá trị của `x; y; z` lần lượt là `-3; -4; -5.`
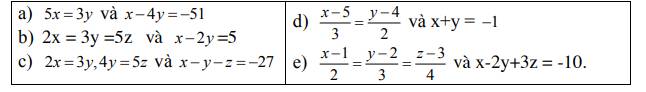
Bài 2 :
\(a,\left(x+2\right)\left(x^2+3x-2\right)=2\left(x+2\right)x^2\)
\(\Leftrightarrow\left(x+2\right)\left(x^2+3x-2\right)-2x^2\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2+3x-2-2x^2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\-x^2+3x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\-x^2+x+2x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\-x\left(x-1\right)+2\left(x-1\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\\left(x-1\right)\left(-x+2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\\left[{}\begin{matrix}x-1=0\\-x+2=0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\end{matrix}\right.\)
Vậy \(S=\left\{-2;2;1\right\}\)
\(b,9x^2-\left(6x+2\right)\left(x-5\right)=1\)
\(\Leftrightarrow9x^2-\left(6x^2-30x+2x-10\right)-1=0\)
\(\Leftrightarrow9x^2-6x^2+30x-2x+10-1=0\)
\(\Leftrightarrow3x^2+28x+9=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=-9\end{matrix}\right.\)
Vậy \(S=\left\{-\dfrac{1}{3};-9\right\}\)
\(c,\dfrac{x}{3x-2}-\dfrac{x}{2+3x}=\dfrac{6x^2}{9x^2-4}\left(dkxd:x\ne\pm\dfrac{2}{3}\right)\)
\(\Leftrightarrow\dfrac{x}{3x-2}-\dfrac{x}{3x+2}-\dfrac{6x^2}{\left(3x-2\right)\left(3x+2\right)}=0\)
\(\Leftrightarrow\dfrac{x\left(3x+2\right)-x\left(3x-2\right)-6x^2}{\left(3x-2\right)\left(3x+2\right)}=0\)
\(\Leftrightarrow3x^2+2x-3x^2+2x-6x^2=0\)
\(\Leftrightarrow4x-6x^2=0\)
\(\Leftrightarrow-2x\left(-2+3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x=0\\-2+3x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tmdk\right)\\x=\dfrac{2}{3}\left(ktmdk\right)\end{matrix}\right.\)
Vậy \(S=\left\{0\right\}\)
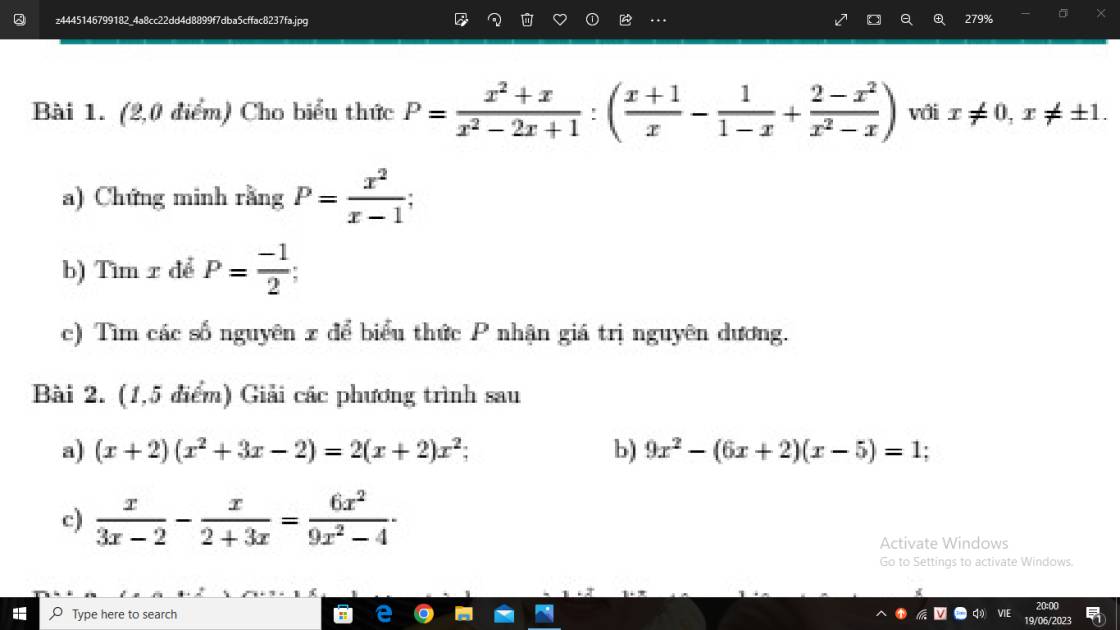
Bài 1 :
\(a,P=\dfrac{x^2+x}{x^2-2x+1}:\left(\dfrac{x+1}{x}-\dfrac{1}{1-x}+\dfrac{2-x^2}{x^2-x}\right)\left(dkxd:x\ne0,x\ne\pm1\right)\)
\(=\dfrac{x^2+x}{\left(x-1\right)^2}:\left(\dfrac{x+1}{x}+\dfrac{1}{x-1}+\dfrac{2-x^2}{x\left(x-1\right)}\right)\)
\(=\dfrac{x^2+x}{\left(x-1\right)^2}:\left(\dfrac{x^2-1+x+2-x^2}{x\left(x-1\right)}\right)\)
\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}.\dfrac{x\left(x-1\right)}{x+1}\)
\(=\dfrac{x^2}{x-1}\left(dpcm\right)\)
\(b,P=-\dfrac{1}{2}\Rightarrow\dfrac{x^2}{x-1}=-\dfrac{1}{2}\)
\(\Rightarrow2x^2=-\left(x-1\right)\)
\(\Rightarrow2x^2=-x+1\)
\(\Rightarrow2x^2+x-1=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-1\end{matrix}\right.\)
Vậy \(P=-\dfrac{1}{2}\) thì \(x=\dfrac{1}{2};x=-1\)
\(c,\) Để P nhận giá trị nguyên dương thì \(P\ge0\)
\(\Leftrightarrow\dfrac{x^2}{x-1}\ge0\Leftrightarrow x\ge0\)