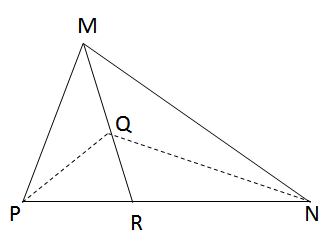
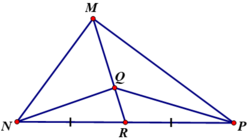
Cho tam giác MNP với đường trung tuyến MR và trọng tâm Q
a) Tính tỉ số các diện tích của hai tam giác MPQ VÀ RPQ
b) Tính tỉ số các diện tích của hai tam giác MNQ và RNQ
c) So sánh các diện tích của hai tam giác RPQ và RNQ
Từ các kết quả trên ,hãy chứng minh các tam giác QMN ,QNP ,QPM có cùng diện tích
Gợi ý: hai tam giác ở mỗi câu a,b,c có chung đường cao

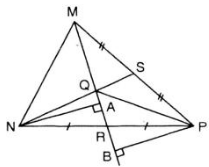


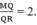
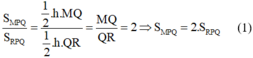
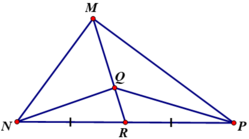
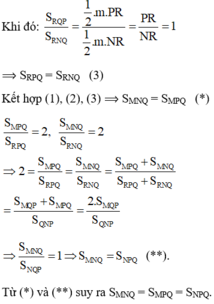
a) Vẽ PB ⊥ MR
Vậy tam giác MPQ và RPQ có chung đường cao PB
Vì Q là trọng tâm của ΔMNR nên MQ = 2QR
Ta có :
\(S\Delta MPQ=\frac{1}{2}MQ.PB=\frac{1}{2}.2QR.PB=QR.PB\)
\(S\Delta RPQ=\frac{1}{2}QR.PB\)
Vậy \(\frac{S\Delta MPQ}{S\Delta RPQ}=\frac{QR.PB}{\frac{1}{2}QR.PB}=2\)
b) Vẽ NA ⊥ MR
Vậy NA là đường cao của ΔMNQ đồng thời là đường cao của ΔRNQ.
Vì Q là trọng tâm của ΔMNP nên MQ = 2QR
Ta có :
\(S\Delta MNQ=\frac{1}{2}MQ.NA=\frac{1}{2}.2QR.NA=QR.NA\)
\(S\Delta RNQ=\frac{1}{2}QR.NA\)
Vậy \(\frac{S\Delta MNQ}{S\Delta RNQ}=\frac{QR.NA}{\frac{1}{2}QR.NA}=2\)
c) \(\Delta NRA=\Delta PRB\) => NA=PB
Ta có :\(S\Delta RPQ=\frac{1}{2}QR.PB=\frac{1}{2}QR.NA=S\Delta RNQ\)
Vậy SΔRPQ = SΔRNQ
- Từ kết quả câu a) ta có:
SΔQPM = 2SΔPRQ = SΔQNP (do câu c) (*)
- Từ kết quả câu b) ta có:
SΔQMN = 2SΔRNQ = SΔQNP (**)
Từ (*) và (**) suy ra:
SΔQMN = SΔQNP = SΔQPM (đpcm)