Cho hình chữ nhật ABCD (AB = 16 cm; BC = 12 cm), M là trung điểm của BC. Lấy điểm P trên cạnh AB và điểm Q trên cạnh CD sao cho AP = CQ. Tính diện tích tam giác PMQ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 8 2021
A B D C M
Chu vi HCN ABCD là:
(32+16)x2=96(cm)
MC=\(\dfrac{1}{2}\)DC=\(\dfrac{1}{2}\)AB
=32:2=16(cm)
Diện tích tam giác ACM là:
16x16=256(cm)
Chúc học tốt
=
T
6
5 tháng 1 2017
Diện tích HCN ABCD là : 20 x 16 = 320 ( cm vuong )
Diện tích hình tam giác AMN là : 10 x 8 : 2 = 40 ( cm vuong )
Diện tích hình tam giác MDC la : 20 x 8 : 2 = 80 ( cm vuong )
Diện tích hình tam giác NBC la : 10 x 16 : 2 = 80 ( cm vuong )
Diện tích hình tam giác MNC la : 320 - ( 40 + 80 + 80 ) = 120 ( cm vuong )
Đáp số : 120 cm vuông
5 tháng 1 2017
Diện tích HCN ABCD là :
20*16=320(cm2 )
Diện tích hình tam giác AMN là :
10*8:2=40(cm2 )
Diện tích hình tam giác MDC là :
20*8:2=80(cm2 ).
Diện tích hình tam giác NBC là:
10*16:2=80(cm2 ).
Diện tích hình tam giác MNCla:
320-(40+80+80)=120(cm2 ).
5 tháng 5 2022
a) 4 hình B) ( 32 + 16 ) x 2 = 96 cm2 C) cạnh DM : 32 :2 = 16 cm, diện tích hình tam giác ADM là : 16 x 16 : 2 = 128 cm2
PT
0
31 tháng 1 2019
Tự vẽ
Nối M với D và N với C như hình vẽ.
Ta có: S NCM = 1/3S DMC (2 tam giác có chiều cao hạ từ C và M bằng nhau và đáy MN=1/3 DC)
Mặt khác, 2 tam giác này lại có chung đáy CM nên chiều cao hạ từ N của tam giác MNC bằng 1/3 chiều cao hạ từ D của tam giác MDC.
Xét 2 tam giác MNO và MDO có chung đáy MO mà chiều cao hạ từ N bằng 1/3 chiều cao hạ từ D nên S MNO =1/3S MDO. Vậy diện tích MNO là 1 phần thì diện tích MDO gồm 3 phần như thế.
Độ dài MN là: 36 : 3 = 12(cm)
Diện tích MND là: 16 x 12 : 2 = 96 (cm2)
Diện tích MNO là: 96 : (1 + 3) = 24 (cm2)
Đ/s: 24 cm2
8 tháng 5 2016
Cạnh AD dài là:16x5/8=10(cm)
Cạnh MB dài là:16:2=8(cm)
Diện tích tam giác MBC là:(10x8):2=40(cm2)
Đáp số:40 cm2
29 tháng 1 2024
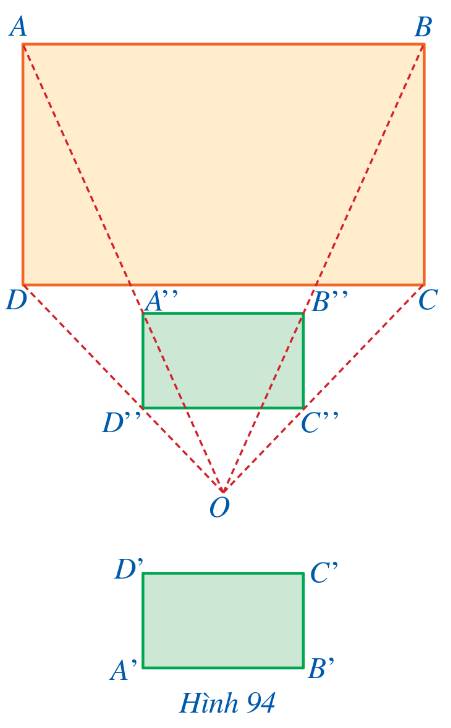
a: Xét ΔODC có D''C''//DC
nên \(\dfrac{D''C''}{DC}=\dfrac{OD''}{OD}=\dfrac{OC''}{OC}=\dfrac{3}{9}=\dfrac{1}{3}\)(1)
Xét ΔOAB có A''B"//AB
nên \(\dfrac{A"B"}{AB}=\dfrac{OA"}{OA}=\dfrac{OB"}{OB}=\dfrac{3}{9}=\dfrac{1}{3}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{OD"}{OD}=\dfrac{OC"}{OC}=\dfrac{OA"}{OA}=\dfrac{OB"}{OB}\)
mà A"A, B"B, C"C, D"D đều đi qua điểm O
nên hai hình hộp chữ nhật A"B"C"D" và ABCD đồng dạng phối cảnh với nhau
b: ta có: A'B'=C'D'=3cm
A"B"=C"D"=3cm
Do đó: A"B"=C"D"=A'B'=C'D'(3)
ta có: A'D'=B'C'=2cm
A"D"=B"C"=2cm
Do đó: A'D'=B'C'=A"D"=B"C"(4)
Từ (3),(4) suy ra hai hình hộp chữ nhật A"B"C"D" và A'B'C'D' bằng nhau