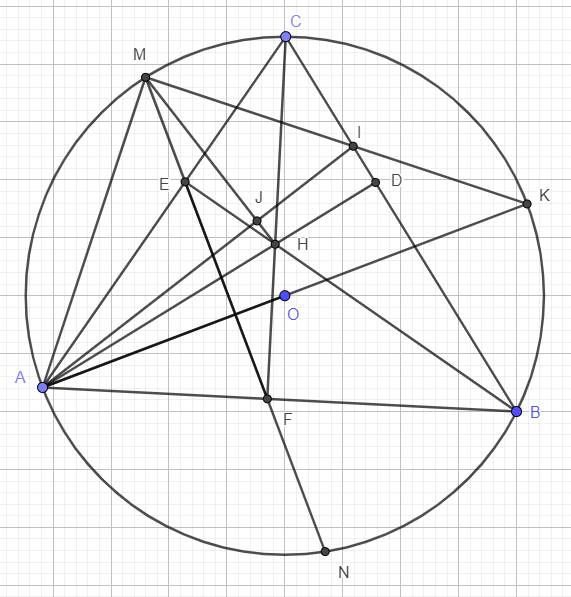
Cho tam giác ABC nối tiếp (O), có ba đường cao AD, BE, CF cắt nhau tại H. Đường thẳng EF cắt hai cung nhỏ AB, AC tại N, M. Vẽ đường kính AK của (O), I là giao điểm của MK với BC, chứng minh AI vuông góc với HM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 4 2020
Giải chi tiết:
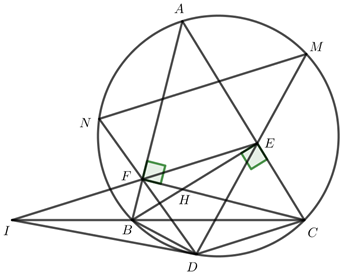
a) Chứng minh tứ giác AEHF và BCEF nội tiếp.
Ta có ∠AEH=∠AFH=90o⇒∠AEH=∠AFH=90o⇒ E, F thuộc đường tròn đường kính AH
⇒⇒ A, E, H, F cùng thuộc một đường tròn
⇒AEHF⇒AEHF là tứ giác nội tiếp (dhnb).
Ta có ∠BEC=∠BFC=90o⇒∠BEC=∠BFC=90o⇒ BCEF là tứ giác nội tiếp (dhnb)
b) Hai đường thẳng EF và BC cắt nhau tại I. Vẽ tiếp tuyến ID với (O)(O)(D là tiếp điểm, D thuộc cung nhỏ BC). Chứng minh ID2=IB.ICID2=IB.IC.
Xét ΔIBDΔIBD và ΔIDCΔIDC có:
∠I∠I chung
∠IDB=∠ICD∠IDB=∠ICD (ID là tiếp tuyến của (O)(O))
⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).
c) DE, DF cắt đường tròn (O)(O) tại M và N. Chứng minh NM // EF.
Xét ΔIBEΔIBE và ΔIFCΔIFC có:
∠I∠I chung
∠IEB=∠ICF∠IEB=∠ICF (BCEF là tứ giác nội tiếp)
⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF (kết hợp b)
⇒ID2=IE.IF⇒IDIE=IFID⇒ID2=IE.IF⇒IDIE=IFID
Xét ΔIDFΔIDF và ΔIEDΔIED có:
∠I∠I chung
IDIE=IFID(cmt)IDIE=IFID(cmt)
⇒ΔIDF∼ΔIED⇒∠IDF=∠IED⇒ΔIDF∼ΔIED⇒∠IDF=∠IED (2 góc tương ứng)
Mặt khác ∠IDF=∠NMD∠IDF=∠NMD (ID là tiếp tuyến của (O)(O)) ⇒∠IED=∠NMD⇒∠IED=∠NMD (tc)
Mà hai góc này ở vị trí đồng vị ⇒⇒ NM // EF.
12 tháng 3 2021
Gọi G là giao điểm của FC và AK.
Áp dụng định lý Menelaus cho tam giác FBC với cát tuyến A, G, K ta có:
\(\dfrac{AF}{AB}.\dfrac{KB}{KC}.\dfrac{GC}{GF}=1\Rightarrow\dfrac{GC}{GF}=\dfrac{KC}{KB}.\dfrac{AB}{AF}\). (1)
Áp dụng định lý Menelaus cho tam giác ACB với cát tuyến K, E, F ta có:
\(\dfrac{EA}{EC}.\dfrac{KC}{KB}.\dfrac{FB}{FA}=1\Rightarrow\dfrac{KC}{KB}=\dfrac{FA}{FB}.\dfrac{EC}{EA}\). (2)
Từ (1), (2) có \(\dfrac{GC}{GF}=\dfrac{EC}{EA}.\dfrac{AB}{FB}\). (*)
Mặt khác áp dụng định lý Menelaus cho tam giác AFC với cát tuyến B, H, E ta có:
\(\dfrac{HC}{HF}.\dfrac{BF}{BA}.\dfrac{EA}{EC}=1\Rightarrow\dfrac{HC}{HF}=\dfrac{AB}{FB}.\dfrac{EC}{EA}\). (**)
Từ (*), (**) ta có \(\dfrac{GC}{GF}=\dfrac{HC}{HF}\Rightarrow\dfrac{AC}{MF}=\dfrac{AC}{NF}\Rightarrow FM=FN\).
1 tháng 3 2019
Giải:
Câu a)
- 2 tam giác vuông ∆ADC và ∆BEC, có góc ADC = góc BEC = 90°, và 2 tam giác vuông này có chung góc C. Từ đây, suy ra => tam giác ∆ADC và tam giác ∆BEC đồng dạng (theo dạng tam giác đồng dạng: góc - góc - góc). Vì ∆ADC và ∆BEC đồng dạng nhau, nên ta có tỷ lệ: DC:EC = AC:BC.
Từ đây, suy ra: DC:AC = CE:BC (1).
Vì tam giác ∆ABC và ∆EDC có chung góc C, và vì kết quả ở (1), nên ta suy ra: ∆ABC và ∆EDC đồng dạng. Từ đây, ta biết được: góc DEC = ABC và góc EDC = góc BAC.
Mà, góc AED + góc DEC = 180° => góc AED + góc ABC = 180° => tứ giác ABDE nội tiếp được một đường tròn (Theo tính chất của tứ giác nội tiếp: 2 góc đối bù nhau).
Câu b)
Chứng minh tương tự như câu a), ta sẽ có:
∆DEC đồng dạng ∆DBF đồng dạng ∆AEF (1)
Từ (1), ta suy ra: góc AEF = góc DEC, mà góc BEA = góc BEC = 90°, nên ta tính được góc BEF = góc BED, suy ra => BE là đường phân giác góc DEF.
Giải tương tự như trên, ta sẽ chứng minh được AD, CF lần lượt là đường phân giác của các góc FDE và góc DFE.
Từ đó, suy ra => H là tâm đường tròn nội tiếp tam giác DEF.