Cho nửa đường tròn ( O ) với đường kính là AB và C là điểm chính giữa cũng AB. Trên cung AC lấy điểm M tùy ý, đường thẳng AM cắt đường thẳng BC tại D. a) C/minh: góc DMC = gíc ABC b) Trên tia BM lấy điểm N sao cho BN = AM C/minh: MC = NC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 5 2021
1: Ta có \(\widehat{CDE}=\widehat{CNE}=90^o\) nên tứ giác CDNE nội tiếp đường tròn đường kính CE.
2: Xét tam giác \(BKD\) và tam giác \(EKM\) có: \(\widehat{BKD}=\widehat{EKM}\) (đối đỉnh), \(\widehat{BDK}=\widehat{EMK}\) (= \(90^o\))
Do đó \(\Delta BKD\sim\Delta EKM(g.g)\).
Suy ra \(\dfrac{KB}{KD}=\dfrac{KE}{KM}\Rightarrow KB.KM=KE.KD\).
Do K là trực tâm của tam giác BCE nên C, K, N thẳng hàng.
3: Ta có \(\widehat{FNK}=\dfrac{1}{2}sđ\stackrel\frown{NC}=\widehat{NBC}=90^o-\widehat{BED}=\widehat{NKF}\). Suy ra tam giác NKF cân tại F nên FN = FK. Lại có tam giác ENK vuông tại N nên F là trung điểm của EK.
Vậy ta có đpcm.
31 tháng 7 2023
a: góc AMB=góc ACB=90 độ
=>BM vuông góc DA và AC vuông góc DB
góc DMH+góc DCH=90+90=180 độ
=>DMHC nội tiếp
Xét ΔHMA vuông tại M và ΔHCB vuông tại C có
góc MHA=góc CHB
=>ΔHMA đồng dạng với ΔHCB
=>HM/HC=HA/HB
=>HM*HB=HA*HC
b: góc DBM=góc CBM=1/2*sđ cung CM
góc MBA=1/2*sđ cung MA
mà sđ cung CM=sđ cung MA
nên góc DBM=góc ABM
=>BM là phân giác của góc DBA
Xét ΔBDA có
BM vừa là đường cao, vừa là phân giác
=>ΔBDA cân tại B
d: Xét ΔMAK vuông tại M và ΔMDH vuông tại M có
MA=MD
góc MAK=góc MDH
=>ΔMAK=ΔMDH
=>MK=MH
Xét tứ giác AKDH có
M là trung điểm chung của AD và KH
AD vuông góc KH
=>AKDH là hình thoi
26 tháng 5 2021
b) Dễ thấy C là trực tâm của tam giác IAB nên C, I, H thẳng hàng.
Do tứ giác AICK là hình thang nội tiếp được đường tròn nên là hình thang cân.
Khi đó \(\widehat{IAK}=\widehat{CKA}\Rightarrow\widehat{IAB}=\widehat{NBA}\)
Suy ra tam giác NAB vuông cân tại N nên \(\widehat{NBA}=45^o\).
Ta có các tứ giác CMIN, AMIH nội tiếp được nên \(\widehat{NMH}=\widehat{NMI}+\widehat{HMI}=\widehat{ICN}+\widehat{IAB}=45^o+45^o=90^o\Rightarrow MN\perp MH\).
26 tháng 5 2021
c) Đề phải là \(\dfrac{IC}{IH}+\dfrac{IA}{IN}+\dfrac{IB}{IM}\ge6\).
Đặt \(x=\dfrac{IH}{CH};y=\dfrac{IN}{AN};z=\dfrac{IM}{BM}\left(x,y,z< 1\right)\).
Ta có \(x+y+z=\dfrac{S_{IAB}}{S_{ABC}}+\dfrac{S_{IBC}}{S_{ABC}}+\dfrac{S_{ICA}}{S_{ABC}}=1\).
Lại có \(\dfrac{IH}{CH}=x\Rightarrow\dfrac{CH}{IH}=\dfrac{1}{x}\Rightarrow\dfrac{IC}{IH}=\dfrac{1}{x}-1\).
Tương tự \(\dfrac{IA}{IN}=\dfrac{1}{y}-1;\dfrac{IB}{IM}=\dfrac{1}{z}-1\).
Do đó \(\dfrac{IC}{IH}+\dfrac{IA}{IN}+\dfrac{IB}{IM}=\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}-3\ge_{Svacxo}\dfrac{9}{x+y+z}-3=\dfrac{9}{1}-3=6\).
Vậy ta có đpcm.
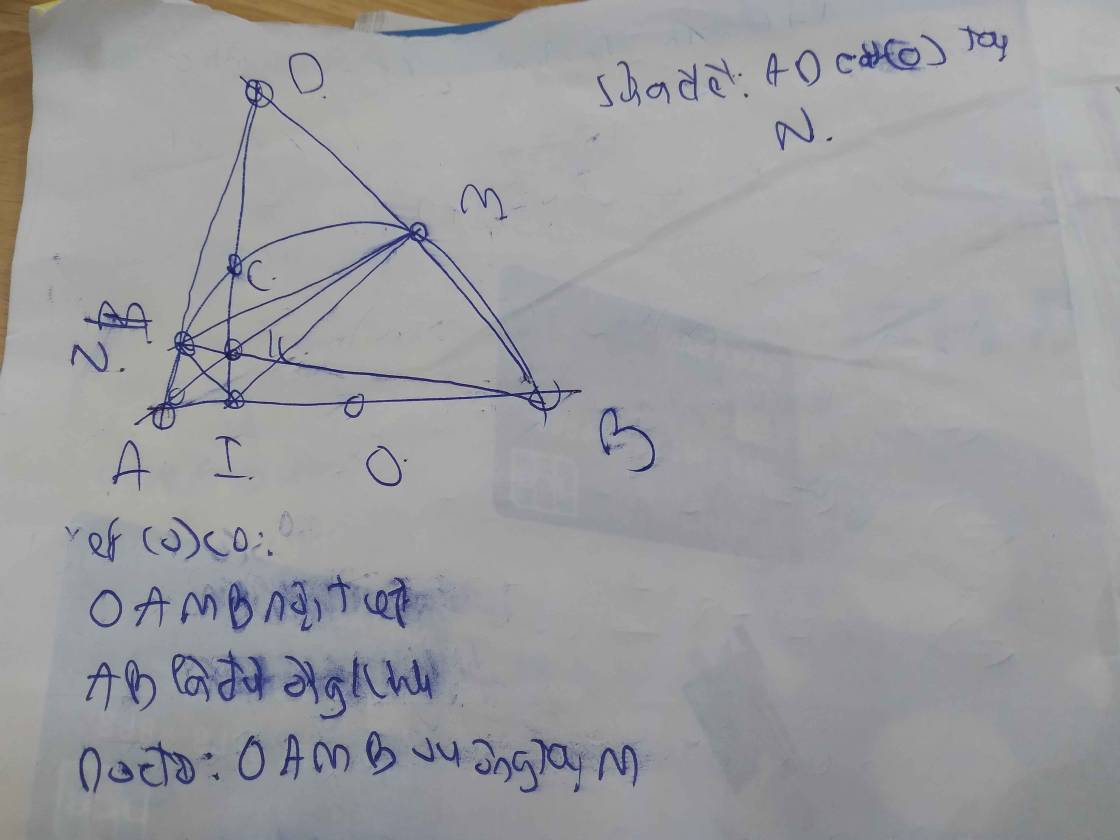
a: góc DMC+góc AMC=180 độ
góc ABC+góc AMC=180 độ
=>góc DMC=góc ABC
b: AC=BC
mà góc NAC=góc NBC và NC chung
nên ΔAMC=ΔBNC
=>MC=NC