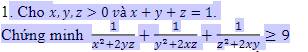 ai làm hộ em với em cần gấp;-;
ai làm hộ em với em cần gấp;-;
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Hình 1:
Áp dụng tslg:
\(cosK=\dfrac{IK}{MK}\)\(\Rightarrow cos42^0=\dfrac{12}{y}\Rightarrow y\approx16,15\)
\(tanK=\dfrac{IM}{IK}\Rightarrow tan42^0=\dfrac{x}{12}\Rightarrow x\approx10,8\)
Hình 2:
\(sinG=\dfrac{HT}{GT}\Rightarrow sin35^0=\dfrac{y}{16}\Rightarrow y\approx9,18\)
\(cosG=\dfrac{GH}{GT}\Rightarrow cos35^0=\dfrac{x}{16}\Rightarrow x\approx10,11\)
Hình 1:
\(x=12\cdot\tan42^0\simeq10.8\left(cm\right)\)
\(y=\sqrt{10.8^2+12^2}\simeq16,14\left(cm\right)\)

bài 2:
T1= 27+273= 300 (K) ; V1=5m3
T2=127+273=400 (K) ; V2=?
quá trình đẳng áp , áp suất p không đổi. Áp dụng mối liên hệ giữu thể tích và nhiệt độ tuyệt đối T ta có:
\(\dfrac{V_1}{T_1}=\dfrac{V_2}{T_2}\Rightarrow V_2=T_2\dfrac{V_1}{T_1}=400\dfrac{5}{300}\simeq6.67\left(m^3\right)\)



Câu 17.
Công ngựa đã thực hiện:
\(A=F\cdot s=200\cdot120=24000J\)
Công suất làm việc của con ngựa:
\(P=\dfrac{A}{t}=\dfrac{24000}{60}=400W\)
Câu 18.
Công đưa vật lên cao:
\(A=P\cdot h=500\cdot0,5=250J\)
Dùng mặt phẳng nghiêng dài 2m cần tối thiểu một lực:
\(F=\dfrac{A}{l}=\dfrac{250}{2}=125N\)
Công để kéo vật lên cao 2m với lực \(F'=150N\) là:
\(A_{tp}=F'\cdot s=150\cdot2=300J\)
Hiệu suất: \(H=\dfrac{A_i}{A_{tp}}\cdot100\%=\dfrac{250}{300}\cdot100\%=83,33\%\)
Công hao phí: \(A_{hp}=A_{tp}-A_i=300-250=50J\)
Lực ma sát:
\(F_{ms}=\dfrac{A_{hp}}{s}=\dfrac{50}{2}=25N\)

a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp
 Ai làm hộ em với ạ e cần gấp ạ
Ai làm hộ em với ạ e cần gấp ạ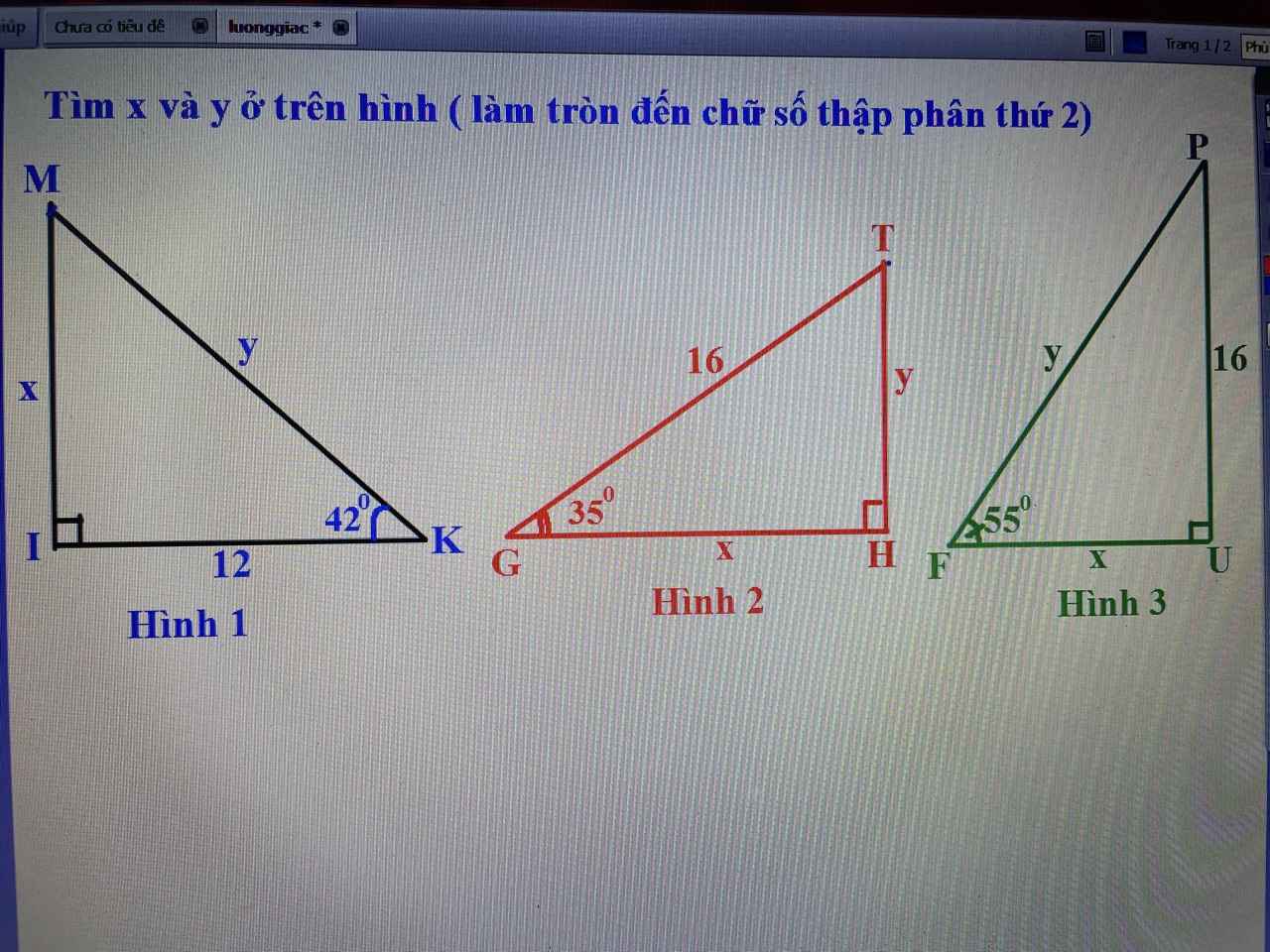







Vì x,y,z>0 nên áp dung bất đẳng thức Cô-si ta có:
\(\dfrac{1}{x^2+2yz}\)+\(\dfrac{1}{y^2+2xz}\)+\(\dfrac{1}{z^2+2xy}\)≥\(\dfrac{\left(1+1+1\right)^3}{x^2+y^2+z^2+2xy+2yz+2xz}\)
mà x+y+z=1 ⇔ x2+y2+z2+2xy+2yz+2zx=1 (bình phương cả 2 vế)
nên \(\dfrac{1}{x^2+2yz}\)+\(\dfrac{1}{y^2+2xz}\)+\(\dfrac{1}{z^2+2xy}\)≥\(\dfrac{\left(1+1+1\right)^2}{\left(x+y+z\right)^2}\)=9