Câu S. (3 điểm) Cho AABC(AB < AC) nhọn nội tiếp (O) có AH là đường cao và I là tâm đường tròn nội tiếp AABC . Gọi T,D lần lượt là giao điểm của Al với BC và (O). a) Chứng minh: OD vuông góc với BC và tam giác IBD cân. ' b) Qua D vẽ đường thẳng vuông góc với AD, cắt AH và BC lần lượt tại P,R. Chứng minh: IP L IR. c) Vẽ IK L BC tại K,DK cắt AH tại S. Chứng minh: tứ giác SIDP nội tiếp.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c: Theo câu b, ta được: H là tâm đường tròn ngoại tiếp ngũ giác DEKFO
OH vuông góc MN
=>MN là đường kính của (H)
=>HM=HN

chứng minh tứ giác OBDK nội tiếp:
dựa vào góc DBK=DOK (vì hai góc cùng chắn cung DK)
vậy, ta cần chứng minh DBK=DOK
đặt giao của OM với AB là H
dễ dàng chứng minh: DBK=BOA=1/2 BOC (1)
có M thuộc (O) và tiếp tuyến CD của M nên chứng minh được tam giác OBD=OMD (ch,cgv)
=> góc BOD=DOM và MOE=COE (chứng minh tương tự)
=> DOM+EOM=DOE=1/2BOM+1/2MOC=1/2BOC (2)
từ (1),(2) => DOK=KBD (đpcm)

CM dễ vãi, AB, AC cắt nhau. Đường kính cất đường tròn tại giao D vs E

a: Xét (O) có
ΔBFC nội tiếp
BC là đường kính
Do đó: ΔBFC vuông tại F
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét ΔABC có
BE,CF là đường cao
BE cắt CF tại H
Do đó: AH vuông góc với BC tại D
b:
Xét tứ giác CDFA có góc CDA=góc CFA=90 độ
nên CDFA là tứ giác nội tiếp
=>góc BFD=góc BCA
Xét tứ giác BFEC có góc BFC=góc BEC=90 độ
nên BFEC là tứ giác nội tiếp
=>góc AFE=góc ACB
Ta có: góc COE=180 độ-2 góc C
góc EFD=180 độ-góc AFE-góc BFD
=180 độ-2 góc C
=>góc COE=góc EFD
=>DOEF là tứ giác nội tiếp
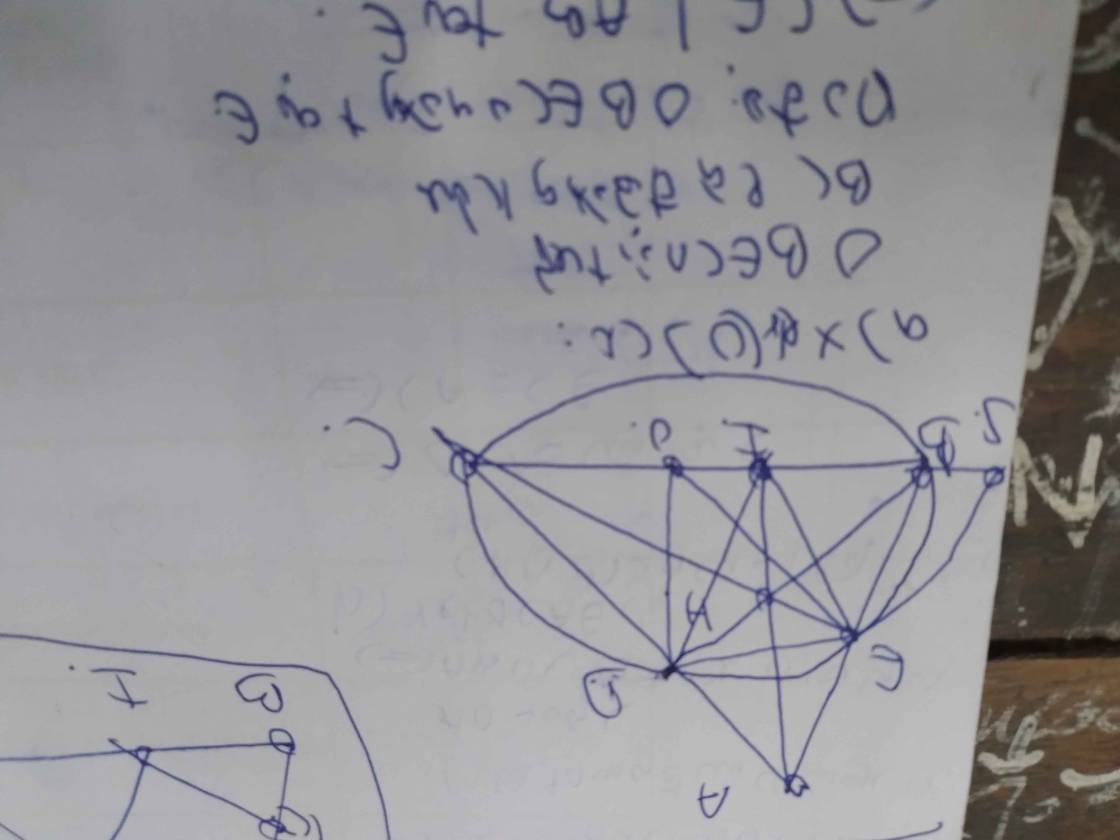


(a) + Ta có : \(OB=OC=R\Rightarrow O\) thuộc đường trung trực của \(BC.\)
Do \(I\) là tâm đường tròn nội tiếp \(\Delta ABC\) nên \(AI\) hay \(AD\) là đường phân giác của
\(\hat{BAC}\Rightarrow\hat{BAD}=\hat{DAC}\Rightarrow\stackrel\frown{BD}=\stackrel\frown{CD}\) (các góc nội tiếp bằng nhau chắn các cung bằng nhau) \(\Rightarrow BD=CD\Rightarrow D\) thuộc đường trung trực của \(BC\).
Từ đó, suy ra \(OD\) là đường trung trực của \(BC\Rightarrow OD\perp BC\) (đpcm).
+ Ta có : \(\hat{DBC}=\hat{DAC}=\hat{BAD}\) (hai góc nội tiếp cùng chắn cung \(CD\) và chứng minh trên). Mà : \(\hat{ABI}=\hat{IBC}\) (do \(I\) là tâm đường tròn nội tiếp \(\Delta ABC\Rightarrow BI\) là phân giác của \(\hat{ABC}\)).
Ta sẽ có được : \(\hat{DBC}+\hat{IBC}=\hat{BAD}+\hat{ABI}\)
\(\Leftrightarrow\hat{IBD}=\hat{BID}\) (\(\hat{BID}\) là góc ngoài của \(\Delta ABI\))
\(\Rightarrow\Delta IBD\) cân tại \(D\) (đpcm).
(b) Xét \(\Delta PAD,\Delta DTR:\) \(\left\{{}\begin{matrix}\hat{PDA}=\hat{TDR}=90^o\left(gt\right)\\\hat{PAD}=\hat{DRT}\end{matrix}\right.\) (cùng phụ với \(\hat{HTA}=\hat{DTR}\) (đối đỉnh))
\(\Rightarrow\Delta PAD\sim\Delta DTR\left(g.g\right)\Leftrightarrow\dfrac{PD}{DT}=\dfrac{AD}{DR}\Leftrightarrow DT.DA=PD.DR\left(1\right).\)
Xét \(\Delta DBT,\Delta DAB:\left\{{}\begin{matrix}\hat{ADB}\text{ chung}\\\hat{DBT}=\hat{DAB}\left(=\hat{BAD}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta DBT\sim\Delta DAB\left(g.g\right)\Leftrightarrow\dfrac{DT}{DB}=\dfrac{DB}{DA}\Leftrightarrow DB^2=DT.DA\left(2\right).\)
Từ \(\left(1\right),\left(2\right)\Rightarrow PD.DR=DB^2=DI^2\) (\(\Delta IDB\) cân tại \(D\left(cmt\right)\Rightarrow DB=DI\)) \(\Leftrightarrow\dfrac{PD}{DI}=\dfrac{DI}{DR}\).
Xét \(\Delta PDI,\Delta IDR:\left\{{}\begin{matrix}\dfrac{PD}{DI}=\dfrac{DI}{DR}\left(cmt\right)\\\hat{PDI}=\hat{IDR}=90^o\end{matrix}\right.\)
\(\Rightarrow\Delta PDI\sim\Delta IDR\left(c.g.c\right)\Leftrightarrow\hat{IPD}=\hat{DIR}\).
Lại có trong \(\Delta IDP\) vuông tại \(D\) : \(\hat{IPD}+\hat{PID}=90^o\) (hai góc phụ nhau), suy ra : \(\hat{DIR}+\hat{PID}=90^o=\hat{PIR}\)
Vậy : \(IP\perp IR\) (đpcm).
(c) Do \(\left\{{}\begin{matrix}IK\perp BC\\AH\perp BC\end{matrix}\right.\left(gt\right)\Rightarrow IK\left|\right|AH\Rightarrow\dfrac{DI}{DA}=\dfrac{DK}{DS}\) (hệ quả của định lí Ta-lét) \(\Rightarrow\dfrac{DB}{DA}=\dfrac{DK}{DS}\). (do \(\Delta IBD\) cân tại \(D\left(cmt\right)\) nên \(ID=DB\)).
Ta cũng có ở câu (b) : \(\Delta DBT\sim\Delta DAB\left(g.g\right)\Rightarrow\dfrac{DB}{DA}=\dfrac{DT}{DB}=\dfrac{DT}{DI}\).
Từ hai điều trên suy ra : \(\dfrac{DK}{DS}=\dfrac{DT}{DI}\).
Xét \(\Delta DKT,\Delta DSI:\left\{{}\begin{matrix}\dfrac{DK}{DS}=\dfrac{DT}{DI}\left(cmt\right)\\\hat{D}\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta DKS\sim\Delta DSI\left(c.g.c\right)\Rightarrow\hat{DKT}=\hat{DSI}\). Hai góc này ở vị trí đồng vị nên \(TK\left|\right|SI\) hay \(BC\left|\right|SI\).
Ta lại có : \(AH\perp BC\Rightarrow SI\perp AH\Rightarrow\hat{PSI}=90^o.\)
Xét tứ giác \(SIDP:\hat{PSI}+\hat{PDI}=90^o+90^o=180^o\). Đây là hai góc đối nhau, vì vậy, tứ giác \(SIDP\) nội tiếp được một đường tròn (đpcm).