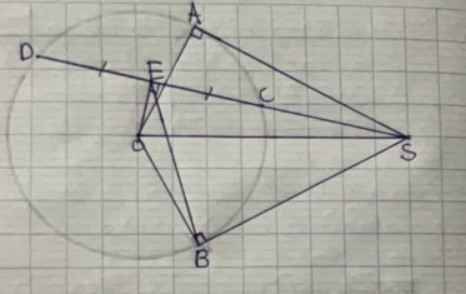
Từ 1 điểm S ở ngoài đường tròn (O) kẻ 2 tiếp tuyến SB, SC ( B, C là tiếp điểm ). Vẽ tia Sx nằm giữa SO và SC cắt đường tròn (O) tại E, F ( E nằm giữa S và F) a) Chứng minh: SC² = SE.SF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔSCE và ΔSFC có
góc SCE=góc SFC
góc CSE chung
=>ΔSCE đồng dạng với ΔSFC
=>SC^2=SE*SF
b: ΔOEF cân tại O
mà OI là trung tuyến
nên OI vuông góc FE
góc OIS+góc OBS=180 độ
=>OISB nội tiếp

a.
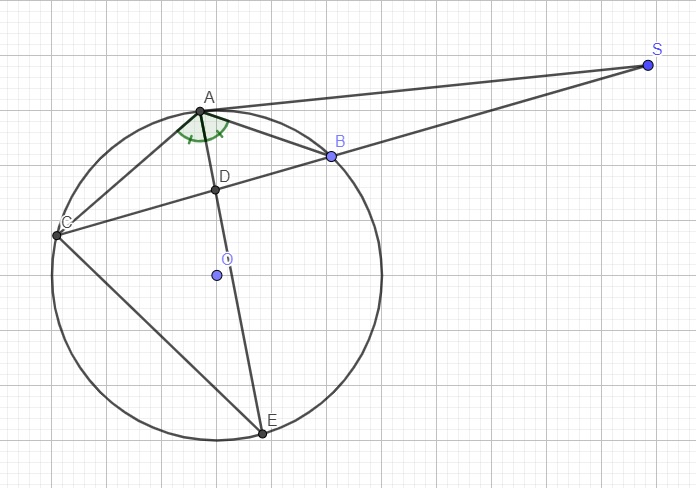
Ta có \(\widehat{SAD}=\widehat{ACE}\) (góc nội tiếp và góc tiếp tuyến cùng chắn cung AE)
Lại có \(\widehat{ADB}\) là góc có đỉnh nằm trong đường tròn
\(\Rightarrow\widehat{ADB}=\dfrac{1}{2}\left(sđ\stackrel\frown{AB}+sđ\stackrel\frown{CE}\right)=\widehat{ACB}+\widehat{CAE}\)
Mà \(\widehat{ACB}=\widehat{SAB}\) (cùng chắn cung AB) và \(\widehat{CAE}=\widehat{BAE}\) (do AE là phân giác \(\widehat{BAC}\))
\(\Rightarrow\widehat{ADB}=\widehat{SAB}+\widehat{BAE}=\widehat{SAD}\Rightarrow\Delta SAD\) cân tại S
\(\Rightarrow SA=SD\)
b.
Xét hai tam giác SAB và SCA có:
\(\left\{{}\begin{matrix}\widehat{ASB}\text{ chung}\\\widehat{SAB}=\widehat{ACB}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta SAB\sim\Delta SCA\left(g.g\right)\)
\(\Rightarrow\dfrac{SA}{SC}=\dfrac{SB}{SA}\Rightarrow SA^2=SB.SC\)
Theo câu a ta có \(SA=SD\)
\(\Rightarrow SD^2=SB.SC\)

Xét tứ giác SOAB có: \(\left\{{}\begin{matrix}\widehat{SAO}=90^o\\\widehat{SBO}=90^o\end{matrix}\right.\)
=> Tứ giác SOAB nội tiếp (tổng 2 góc đối = 180o).
=> 4 điểm S, A, O, B cùng thuộc 1 đường tròn.




a: Xét ΔSCE và ΔSFC có
góc SCE=góc SFC
góc CSE chung
=>ΔSCE đồng dạng với ΔSFC
=>SC^2=SE*SF