Hai lực có giá đồng quy có độ lớn là 10N và 15N và có phương vuông góc với nhau. Hợp lực của hai lực này có độ lớn là bao nhiêu? A. 5N. B. 25N. C. 5√13N. D. 150N
có giải thích cách giải luôn ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
24 tháng 2 2018
Trong phép tổng hợp hai lực thì hai lực thành phần cùng với hợp lực tạo thành một hình tam giác. Độ lớn của các lực biểu diễn bằng độ dài của các cạnh tam giác đó.
Từ định lí hàm số cosin đối với tam giác, áp dụng cho trường hợp này ta có góc giữa hai lực đồng quy xác định bởi:
VT
7 tháng 12 2019
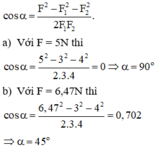
Chọn đáp án C
Hai lực thành phần F1 = F2 hợp nhau bất kỳ thì hợp lực:
VT
5 tháng 3 2019
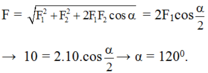
Ta có, hợp lực của hai lực thành phần
F = F 1 2 + F 2 2 + 2 F 1 F 2 c o s α
Thay số vào, ta được
F = F 1 2 + F 2 2 + 2 F 1 F 2 c o s α = 10 2 + 10 2 + 2.10.10 cos 60 0 = 103 N ≈ 17 , 32 N
Đáp án: A
VT
12 tháng 4 2019
Ta có F 2 = F 1 2 + F 2 2 + 2 F 1 F 2 cos α
7 , 8 2 = 4 2 + 5 2 + 2.4.5. cos α ⇒ α = 60 , 26 0
26 tháng 11 2023
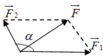
a:
Gọi hai lực đồng quy đề bài cho lần lượt là \(\overrightarrow{F_1};\overrightarrow{F_2}\)
Gọi hợp lực của \(\overrightarrow{F_1};\overrightarrow{F_2}\) là \(\overrightarrow{F}\)
Do đó, ta có: \(\overrightarrow{F}=\overrightarrow{F_1}+\overrightarrow{F_2}\)
=>\(\left|\overrightarrow{F}\right|=\sqrt{F_1^2+F_2^2+2\cdot F_1\cdot F_2\cdot cos\left(\overrightarrow{F_1},\overrightarrow{F_2}\right)}\)
=>\(F=\sqrt{18^2+24^2+2\cdot18\cdot24\cdot cos25}\simeq41,02\left(N\right)\)
b: \(F=31N\)
=>\(\sqrt{F_1^2+F_2^2+2\cdot F_1\cdot F_2\cdot cos\left(\overrightarrow{F_1};\overrightarrow{F_2}\right)}=31\)
=>\(900+2\cdot18\cdot24\cdot cos\left(\overrightarrow{F_1};\overrightarrow{F_2}\right)=961\)
=>\(864\cdot cos\left(\overrightarrow{F_1};\overrightarrow{F_2}\right)=61\)
=>\(cos\left(\overrightarrow{F_1};\overrightarrow{F_2}\right)=\dfrac{61}{864}\)
=>\(\left(\overrightarrow{F_1};\overrightarrow{F_2}\right)\simeq86^0\)
Hợp lực F có giới hạn:
\(\left|F_1-F_2\right|\le F\le\left|F_1+F_2\right|\)
\(\Leftrightarrow\left|10-15\right|\le F\le\left|10+15\right|\)
\(\Leftrightarrow5N\le F\le25N\)
\(\Rightarrow\) Chọn A, B, C