Cho tam giác ABC,trên cạnh BC lấy điểm M. Qua điểm M kẻ các đường thẳng song song với AC và AB thứ tự cắt AB và AC tại E và F.1) CM: \(\frac{ME}{AC}\)+\(\frac{MF}{AB}\)có giá trị không đổi2) Cho biết diện tích của các tam giác MBE và MCF thứ tự là \(a^2\)và \(b^2\).Tính diện tích tam giác BC theo a và b3) Xác định vị trí của M để diện tích tứ giác AEMF lớn...
Đọc tiếp
Cho tam giác ABC,trên cạnh BC lấy điểm M. Qua điểm M kẻ các đường thẳng song song với AC và AB thứ tự cắt AB và AC tại E và F.
1) CM: \(\frac{ME}{AC}\)+\(\frac{MF}{AB}\)có giá trị không đổi
2) Cho biết diện tích của các tam giác MBE và MCF thứ tự là \(a^2\)và \(b^2\).Tính diện tích tam giác BC theo a và b
3) Xác định vị trí của M để diện tích tứ giác AEMF lớn nhất
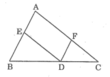
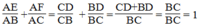
a. Do ME // AC nên \(\frac{ME}{AC}=\frac{BM}{BC}\); MF // AB nên \(\frac{MF}{AB}=\frac{MC}{BC}\)
Từ đó suy ra \(\frac{ME}{AC}+\frac{MF}{AB}=\frac{BM+MC}{BC}=1\) không đổi.
b. Gọi \(\frac{ME}{AC}=t\Rightarrow\frac{MF}{AB}=1-t\Rightarrow S_{ABC}=\frac{a^2}{t^2}=\frac{b^2}{\left(1-t\right)^2}\)
\(\Rightarrow\frac{a}{t}=\frac{b}{1-t}\Rightarrow a\left(1-t\right)=bt\Rightarrow t=\frac{a}{a+b}\Rightarrow t^2=\frac{a^2}{\left(a+b\right)^2}\Rightarrow S_{ABC}=\frac{a^2}{t^2}=\left(a+b\right)^2.\)
c. \(S_{AEMF}=S_{ABC}-S_{BME}-S_{CMF}=\left(a+b\right)^2-a^2-b^2\)
\(=2ab\le a^2+b^2\)
Dấu bằng xảy ra khi a = b, tức là M là trung điểm BC.