vẽ góc xoy có số đo là 70o
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 7 2015
Cho góc XOY có số đo 70o. Tia OZ là tia phân giác của góc XOY. Gọi OT là tia đối của tia OX. Tính so đo góc TOH
H ở đâu thế
13 tháng 4 2020
a)vì góc xOy kề bù vs góc yOz
=)góc xOy+góc yOz=1800
=)700+ góc yOz=1800=)góc yOz=1800-700=1100
b)vì Om là phân giác góc xOy=)góc yOm=1/2 góc xOy=1/2*700=350
c)vì On là phân giác góc yOz=)góc yOn =1/2 góc yOz=1/2*1100=650
mà yOm=350=)yOm+yOn=350+650=900
vậy mOn là goc1 vuông
PT
1
CM
2 tháng 3 2017
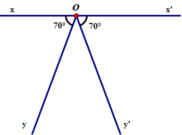
Vẽ hình:
Cách 1: Vẽ đường thằng x’x . Trên x’x lấy điểm O
Vẽ góc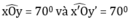 
(Oy và Oy’ cùng thuộc một nửa mặt phẳng bờ xx’).
Cách 2 : Hoặc vẽ góc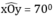 
Từ O vẽ tia Ox’ bất kì (không phải là tia đối của Ox )
CM
19 tháng 6 2017
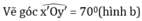
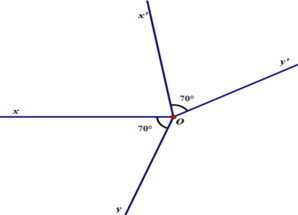
Vì tia Oy nằm giữa hai tia Ox và Oz nên:
∠(xOz) = ∠(xOy) + ∠(yOz)
Ta có: ∠(xOy) = 40o , nếu số đo của ∠(yOz) lần lượt bằng 30o, 50o, 70o, 140o
Thì:
∠(yOz) = 30o ; ∠(xOz) = 40o + 30o = 70o; ∠(xOz) là góc nhọn
∠(yOz) = 50o ; ∠(xOz) = 40o + 50o = 90o; ∠(xOz) là góc vuông
∠(yOz) = 70o ; ∠(xOz) = 40o + 70o = 110o; ∠(xOz) là góc tù
∠(yOz) = 140o ; ∠(xOz) = 40o + 140o = 180o; ∠(xOz) là góc bẹt
AH
Akai Haruma
Giáo viên
29 tháng 12 2022
Lời giải:
a. Hai góc kề bù:
$\widehat{xOy}$ và $\widehat{yOm}$
b.
Vì $\widehat{xOy}$ và $\widehat{yOm}$ kề bù nên:
$\widehat{xOy}+\widehat{yOm}=180^0$
$\widehat{yOm}=180^0-\widehat{xOy}=180^0-60^0=120^0$
c.
Vì $Om$ là phân giác $\widehat{xOy}$ nên $\widehat{yOt}=\widehat{xOt}=\frac{1}{2}\widehat{xOy}=\frac{1}{2}.60^0=30^0$
$\widehat{xOt}$ và $\widehat{tOm}$ là 2 góc kề bù nên:
$\widehat{xOt}+\widehat{tOm}=180^0$
$\widehat{tOm}=180^0-\widehat{xOt}=180^0-30^0=150^0$
18 tháng 9 2023
a) Hai góc kề bù có trên hình vừa vẽ là góc xOy và mOy
b) Vì \(\widehat {xOy} + \widehat {yOm} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {yOm} = 180^\circ \\ \Rightarrow \widehat {yOm} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
c) Vì tia Ot là tia phân giác của góc xOy nên \(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.60^\circ = 30^\circ \)
Mà \(\widehat {xOt}\) và \(\widehat {tOm}\) là hai góc kề bù nên
\(\begin{array}{l}\widehat {xOt} + \widehat {tOm} = 180^\circ \\ \Rightarrow 30^\circ + \widehat {tOm} = 180^\circ \\ \Rightarrow \widehat {tOm} = 180^\circ - 30^\circ = 150^\circ \end{array}\)
Vậy \(\widehat {tOy} = 30^\circ ;\widehat {tOm} = 150^\circ \)
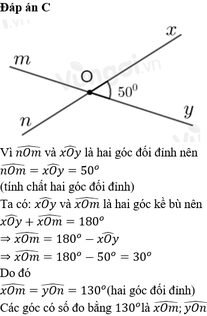
dễ vl