giúp em phần 5.2 với ạ em 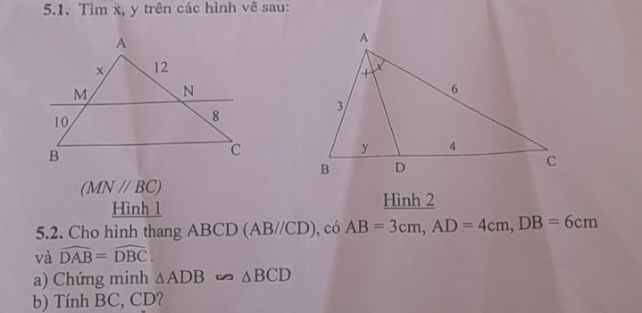 đang gấp
đang gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì khi cài đặt ứng dụng, phải dựa trên hệ điều hành để cài đặt. Phải thay đổi phần mềm ứng dụng sao cho phù hợp với hệ điều hành nếu không, phần mềm sẽ không thể chạy hoặc sẽ bị lỗi khi hoạt động.

Bài 6:
a. \(A=[\frac{\sqrt{x}}{\sqrt{x}-1}+\frac{2}{\sqrt{x}(\sqrt{x}-1)}].(\sqrt{x}-1)\)
\(=\sqrt{x}+\frac{2}{\sqrt{x}}=\frac{x+2}{\sqrt{x}}\)
b. Áp dụng BĐT Cô-si cho các số dương:
$A=\sqrt{x}+\frac{2}{\sqrt{x}}\geq 2\sqrt{2}$
Vậy gtnn của $A$ là $2\sqrt{2}$. Giá trị này đạt tại $x=2$
Bài 7:
a.
\(x=\frac{1}{\sqrt{3}-1}-\frac{1}{\sqrt{3}+1}=1\)
Khi đó: \(B=\frac{1+3}{1+8}=\frac{4}{9}\)
b. \(A=\frac{(\sqrt{x}+1)(\sqrt{x}+3)+\sqrt{x}(2\sqrt{x}-1)}{(2\sqrt{x}-1)(\sqrt{x}+3)}-\frac{x+6\sqrt{x}+2}{(2\sqrt{x}-1)(\sqrt{x}+3)}\)
\(=\frac{3x+3\sqrt{x}+3-(x+6\sqrt{x}+2)}{(\sqrt{x}+3)(2\sqrt{x}-1)}=\frac{2x-3\sqrt{x}+1}{(2\sqrt{x}-1)(\sqrt{x}+3)}\)
\(=\frac{(2\sqrt{x}-1)(\sqrt{x}-1)}{(2\sqrt{x}-1)(\sqrt{x}+3)}=\frac{\sqrt{x}-1}{\sqrt{x}+3}\)
c.
\(P=AB=\frac{\sqrt{x}+3}{x+8}.\frac{\sqrt{x}-1}{\sqrt{x}+3}=\frac{\sqrt{x}-1}{x+8}\)
Áp dụng BĐT Cô-si:
$x+16\geq 8\sqrt{x}$
$\Rightarrow x+8\geq 8(\sqrt{x}-1)$
$\Rightarrow P\leq \frac{\sqrt{x}-1}{8(\sqrt{x}-1)}=\frac{1}{8}$
Vậy $P_{\max}=\frac{1}{8}$ khi $x=16$



Cụm danh từ: những cánh tay săn chắc ấy
Phụ trước: những
Trung tâm: cánh tay
Phụ sau: săn chắc ấy
cụm DT:những ngón tay nhỏ nhắn xinh xắn ấy
Phụ trước: những
Phần trung tâm: ngón tay
Phụ sau: nhỏ nhắn, xinh xắn ấy

Câu 1:
\(\left(4x+3\right)\left(3x^2+x-2\right)\left(2x^2-3x-5\right)=0\\ \Leftrightarrow\left(4x+3\right)\left(3x-2\right)\left(x+1\right)\left(2x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{4}\\x=-1\\x=\dfrac{2}{3}\\x=\dfrac{5}{2}\end{matrix}\right.\\ \Leftrightarrow A=\left\{-1;-\dfrac{3}{4};\dfrac{2}{3};\dfrac{5}{2}\right\}\)
Câu 2:
\(\left(x^2-4\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\\x=3\end{matrix}\right.\Leftrightarrow A=\left\{-2;2;3\right\}\\ \left|5x\right|-11\le0\Leftrightarrow\left|5x\right|\le11\Leftrightarrow-11\le5x\le11\\ \Leftrightarrow-\dfrac{11}{5}\le x\le\dfrac{11}{5}\\ \Leftrightarrow B=\left[-\dfrac{11}{5};\dfrac{11}{5}\right]\)
\(\Leftrightarrow A\cap B=\left\{-2;2\right\}\\ A\cup B=\left[-\dfrac{11}{5};3\right]\\ A\B=\left\{3\right\}\)

Ta có :
\(\frac{x}{3}=\frac{y}{5}\) (1)
\(\left(x+2\right)+\left(y+3\right)=21\)
\(\Leftrightarrow x+2+y+3=21\)
\(\Leftrightarrow x+y=16\)
\(\Leftrightarrow x=16-y\)
Thay x = 16 - y vào (1) ta được :
\(\frac{16-y}{3}=\frac{y}{5}\)
\(\Rightarrow5\left(16-y\right)=3y\)
\(\Leftrightarrow80-5y=3y\)
\(\Leftrightarrow80=8y\)
\(\Leftrightarrow y=10\)
\(\Rightarrow x=16-10=6\)
Vậy x = 6 và y = 10








a) Sửa đề: Chứng minh \(\Delta DAB\) \(\sim\) \(\Delta CBD\)
Xét \(\Delta DAB\) và \(\Delta CBD\) có:
\(\widehat{DAB}=\widehat{CBD}\left(gt\right)\)
\(\widehat{ABD}=\widehat{BDC}\) (so le trong)
\(\Rightarrow\Delta DAB\sim\Delta CBD\left(g-g\right)\)
b) Do \(\Delta DAB\sim\Delta CBD\) (cmt)
\(\Rightarrow\dfrac{AD}{BC}=\dfrac{AB}{BD}=\dfrac{BD}{CD}\)
*) \(\dfrac{AD}{BC}=\dfrac{AB}{BD}\)
\(\Rightarrow BC=\dfrac{AD.BD}{AB}\)
\(=\dfrac{4.6}{3}=8\left(cm\right)\)
*) \(\dfrac{AB}{BD}=\dfrac{BD}{CD}\)
\(\Rightarrow CD=\dfrac{BD.BD}{AB}\)
\(=\dfrac{6.6}{3}=12\left(cm\right)\)