Có thể, chắc chắn hay không thể?
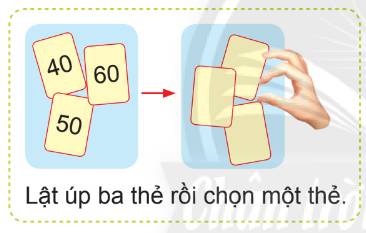
a) Thẻ được chọn .?. có số tròn chục.
b) Thẻ được chọn .?. có số 70.
c) Thẻ được chọn .?. có số 50.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
Biến cố A là biến cố ngẫu nhiên vì các số ghi trên các tấm thẻ có cả số chẵn và số lẻ
Biến cố B là biến cố chắc chắn vì tất cả các tấm thẻ đều ghi số chia hết cho 3
Biến cố C là biến cố không thể vì các số ghi trên các tấm thẻ không có số nào chia hết cho 10.
HQ
Hà Quang Minh
Giáo viên
19 tháng 10 2023
a) Chắc chắn lấy được thẻ ghi số tự nhiên
b) Có thể lấy được thẻ ghi số lẻ
c) Không thể lấy được thẻ ghi số lớn hơn 4 00 000
26 tháng 11 2023
a) Chắc chắn lấy được thẻ ghi số tự nhiên
b) Có thể lấy được thẻ ghi số lẻ
c) Có thể lấy được thẻ ghi số lớn hơn 400 000
c) Vì 3 600 152 và số 492 735 lớn hơn 400 000
HQ
Hà Quang Minh
Giáo viên
8 tháng 10 2023
- Số của thẻ lấy ra là số chẵn: Có thể xảy ra
- Số của thẻ lấy ra là số lẻ: Có thể xảy ra
- Số của thẻ lấy ra chia hết cho 10: không thể xảy ra
- Số của thẻ lấy ra nhỏ hơn 10: Chắc chắn xảy ra.
HQ
Hà Quang Minh
Giáo viên
1 tháng 12 2023
a) Mai có thể đặt số 8 hoặc số 9.
b) Mai có tất cả 2 cách chọn thẻ là chọn thẻ ghi số 8 hoặc thẻ ghi số 9.
CM
19 tháng 8 2019
Trong 20 tấm thẻ từ 1 đến 20 có 10 tấm thẻ mang số lẻ, 10 tấm thẻ mang số chẵn trong đó có 5 tấm thẻ chia hết cho 5. Gọi A là biến cố: " chọn có 3 tấm thẻ mang số lẻ, 2 tấm thẻ mang số chẵn trong đó có ít nhất một tấm thẻ mang số chia hết cho 4"
TH1: Chọn được 3 tấm thẻ mang số lẻ 1 tấm thẻ mang số chẵn chia hết cho 4 và một tấm chẵn mang số không chia hết cho 4 có: 
TH2: Chọn được 3 tấm thẻ mang số lẻ và 2 tấm thẻ mang số chẵn và chia hết cho 4 có:
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
a) Mỗi phần tử của không gian mẫu là một tổ hợp chập 2 của 20 phần tử. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{20}^2\) ( phần tử)
b) Gọi A là biến cố “Tích các số trên hai thẻ là số lẻ”
Để tích các số trên thẻ là số lẻ thì cả hai thẻ bốc được đểu phải là số lẻ vậy nên ta phải chọn ngẫu nhiên 2 thẻ từ 10 thẻ số lẻ. Do đó, số phần tử các kết quả thuận lợi cho biến cố A là tổ hợp chập 2 của 10 phần tử: \(n\left( A \right) = C_{10}^2\) ( phần tử)
Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{10}^2}}{{C_{20}^2}} = \frac{9}{{38}}\)
AH
Akai Haruma
Giáo viên
23 tháng 5 2021
Lời giải:
Trong các số từ 1 đến 30, có $\frac{30-3}{3}+1=10$ số chia hết cho $3$
Do đó, xác suất để chọn được chiếc thẻ chia hết cho $3$ là:
$\frac{10}{30}=\frac{1}{3}$
21 tháng 8 2023
Để lập được nhiều nhất các số lẻ có hai chữ số từ 5 thẻ số 1, 2, 3, 4, 5, Đăng cần chọn ba thẻ số 1, 3 và 5. Khi đó, ta có thể lập được 9 số lẻ có hai chữ số, đó là: 11, 13, 15, 31, 33, 35, 51, 53, 55.
a) Thẻ được chọn chắc chắn có số tròn chục (Vì các số 40, 50, 60 đều là số tròn chục).
b) Thẻ được chọn không thể có số 70 (Vì trong 3 thẻ không có thẻ nào có số 70).
c) Thẻ được chọn có thể có số 50 (Vì trong 3 thẻ có 1 thẻ có số 50).