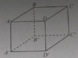
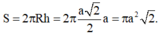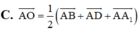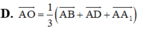Cho hình lập phương ABCD .A'B'C'D' có cạnh là a . Gọi M, N, P lần lượt là trung điểm của cạnh AB ,CC' ,D'A'. Tính d(D;(MNP))
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Dễ thấy (CMN) là (ABC'D')(Vì CM,MN,CN nằm trong mp đó)
thiết diện có S=\(a^2\sqrt{2}\)

Gọi M là trung điểm của BD, là trung điểm của A’B.
Suy ra tâm O của tam giác BDA’ là giao của DN và A’M
Phương án D đúng vì BD ⊥ (AMA') bởi BD ⊥ AM và BD ⊥ A’M ⇒ BD ⊥ AO
BA’ ⊥ (AND) do BA’ ⊥ DN và A’B ⊥ AN ⇒ A’B ⊥ AO
AO ⊥ (A’BD) ⇒ O là hình chiếu của A trên (A’BD).
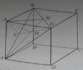
Đáp án D

\(A'C'=\sqrt{a^2+a^2}=a\sqrt{2}\)
=>\(A'C=\sqrt{\left(a\sqrt{2}\right)^2+\left(a\sqrt{3}\right)^2}=a\sqrt{5}\)

a ) Diện tích xung quanh là :
3 x 3 x 4 = 36 (cm2)
b) Diện tích toàn phần là :
3 x 3 x 6 = 54 (cm2)
Đáp số : a )...
b ) .......
a,tính diện tích xung quanh hình lập phương đó là:
3x 3 x 4 =36 ( cm2)
b, tính diện tích toàn phần hình lập phương đó là:
3x3 x 6 =54 ( cm2)

Phương pháp:
Góc giữa hai mặt phẳng là góc giữa 2 đường thẳng lần lượt thuộc hai mặt phẳng và vuông góc với giao tuyến.
Cách giải:
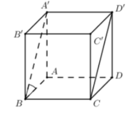
Ta có
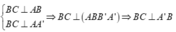
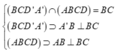
![]()
![]()
Do ABB 'A ' là hình vuông ![]()
![]()
Chọn A.

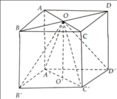
a) Bốn tam giác OAA', OBB', OCC', ODD' là các tam giác vuông bằng nhau nên suy ra OA' = OB' = OC' = OD'.
Hình chóp O.A'B'C'D' là hình chóp đều vì có các mặt bên là tam giác cân và đáy là đa giác đều.
b) Thể tích của của hình chóp O.A'B'C'D' là:
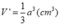
Thể tích hình lập phương:
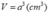
Vậy V ' V = 1 3

Đáp án C
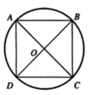
Do hình trụ và hình lập phương có cùng chiều cao nên ta chỉ cần chú ý đến mặt đáy như hình vẽ bên. Đường tròn đáy của hình trụ có bán kính bằng một nửa đường chéo của hình vuông
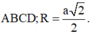 Do đó thể tích hình trụ cần tìm bằng
Do đó thể tích hình trụ cần tìm bằng