một người đẩy thùng hàng có trọng lượng P=1200N, lên độ cao h=2m bằng một mặt phẳng nghiêng dài 8m(bỏ qua ma sát).
a) hãy tính lực tối thiểu mà người đó bỏ ra để đẩy thùng hàng
b) hãy tính công tối thiểu mà người đó đã thực hiện
GIÚP MK VỚI
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tóm tắt:
\(m=10kg\\ l=10m\\ h=2m\\ F_{ms}=20N\\ ----------\\ A=?J\)
Giải:
Công có ích: \(A_{ich}=P.h=\left(10.m\right).h\\ =\left(10.10\right).2=200\left(J\right)\)
Công ma sát: \(A_{ms}=F_{ms}.l\\ =20.10=200\left(J\right)\)
Công của người đẩy (Công toàn phần): \(A_{tp}=A_{ich}+A_{ms}\\ =200+200=400\left(J\right).\)

Lực đẩy
\(F=\dfrac{A}{l}=\dfrac{5000.4}{8}=2500N\)
Công suất
\(P=\dfrac{A}{t}=\dfrac{2500}{45}=55,\left(5\right)W\)
Lực đẩy:
`F = A/l = (5000 xx 4)/8 = 2500 N`.
Công suất:
`P = A/t = 2500/45 = 55, (5) W`.

a) Trọng lượng của thùng hàng là:
\(P=10.m=10.500=5000\left(N\right)\)
Công cần dùng là:
\(A=P.h=5000.1=5000\left(J\right)\)
Lực kéo tối thiểu là:
\(A=P.h=F.l\\ \Rightarrow F=\dfrac{A}{l}=\dfrac{5000}{4}=1250\left(N\right)\)
b) Độ lớn lực ma sát:
\(F_{ms}=P=5000\left(N\right)\)
Lực kéo vật khi này là:
\(F'=F+F_{ms}=1250+5000=6250\left(N\right)\)
Công thực tế là:
\(A'=F'.l=6250.4=25000\left(J\right)\)

Đáp án B
Vì đưa thùng hàng lên cùng độ cao, mà tấm ván thứ hai cần lực kéo nhỏ nhất nên suy ra độ nghiêng của tấm thứ hai nhỏ nhất. Từ đó suy ra chiều dài của tấm ván thứ hai là lớn nhất

Đáp án D
- Trọng lượng thùng hàng là:
50.10 = 500 (N)
- Áp dụng công thức:
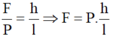
- Lực cần thiết để kéo thùng hàng là:
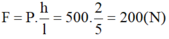

a)Công nâng vật:
\(A=P\cdot h=10m\cdot h=10\cdot200\cdot1=2000J\)
Lực kéo vật:
\(F_k=\dfrac{A}{l}=\dfrac{2000}{5}=400N\)
b)Công kéo vật:
\(A_{tp}=F\cdot l=450\cdot5=2250J\)
Hiệu suất mặt phẳng nghiêng:
\(H=\dfrac{A_i}{A_{tp}}\cdot100\%=\dfrac{2000}{2250}\cdot100\%=88,89\%\)