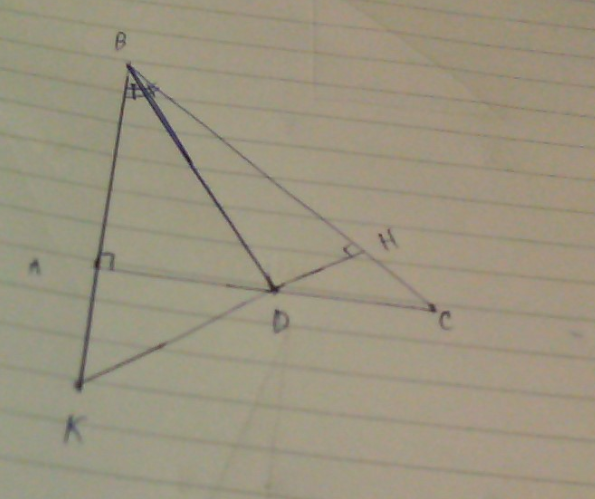
Cho tam giác ABC vuông tai A (AB<AC) có duong cao AH. Goi D,E lan luot là hình chieu cua H lên AB và AC.Goi M là trung diem cua BC
*AD.AB=AH2 =AE.AC
*AD.AC+AE.AB=AB.AC
a) Chung minh :
*DB.DA+EC.EA=AH2
*BD.BA+CE.CA=AB2+AC2-2AH2
b) Chung minh tam giác ADE - tam giác ACB; AM vuông DE tai S và 1/AS=1/HB+1/HC
c)AF là phân giác góc BAH; AJ là phân giác góc CAH.Chung minh: *AB+AC=BC+FJ
*FH.FC=BF.CH
*JH.JB=JC.BH
d) AJ là phân giác cua góc HAC, goi L là trung diem cua AJ,BL cat AH tai N. Trên canh HJlay diem K (HK>KJ), Kéo dài KN cat AB tai Q. Chung minh: BA/BQ+BJ/BK+2.BL/BN
e) Goi X,Y,Z lan luot là tâm các duong phân giác trong cua tam giác ABH,ACH và AHM. Chung minh tam giác HXY-tam giác ABC và tính so đo góc BZM