cho hình chóp S.ABCD có đáy là hình vuông SA vuông góc (ABCD). gọi M là hình chiếu vuông góc của A lên cạnh SB cmr: a, CB vuông góc (SAB) b, AM vuông góc (SBC)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Đề thiếu dữ liệu liên quan đến điểm S (ví dụ SA hay SB vuông góc đáy gì đó)
- Đề sai (A thuộc SA nên không thể tồn tại M là hình chiếu của A lên SA.)

+)CD⊥SA do SA vuông với ABCD
CD⊥AD( tính chất hình vuông)
=>CD⊥(SAD)=>CD⊥AN mà SD⊥AN=> AN⊥(SDC)=>AN⊥SC(1)
+) BC⊥SA do SA vuông với ABCD
BC⊥AB( tính chất hình vuông)
=>BC⊥(SAB)=>BC⊥AM mà SB⊥AM=> AM⊥(SAB)=>AM⊥SC(2)
TỪ 1 và 2 => SC⊥(AMN) đpcm

Đáp án B
Ta có: B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ M A
Mặt khác A M ⊥ S B ⇒ A M ⊥ S B C ⇒ A N ⊥ S C , tương tự A N ⊥ S C
Do đó S C ⊥ A M N , mặt khác ∆ S B C vuông tại B suy ra tan B S C ^ = B C S B = a S A 2 + A B 2 = 1 3
⇒ S B ; S C ^ = B S C ^ = 30 ° ⇒ S B ; A M N ^ = 60 ° .
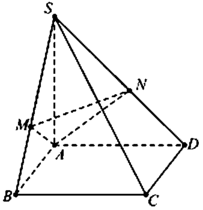
a: CB vuông góc SA
CB vuông góc AB
=>CB vuông góc (SAB)
b: CB vuông góc (SAB)
=>CB vuông góc AM
mà AM vuông góc SB
nên AM vuông góc (SBC)