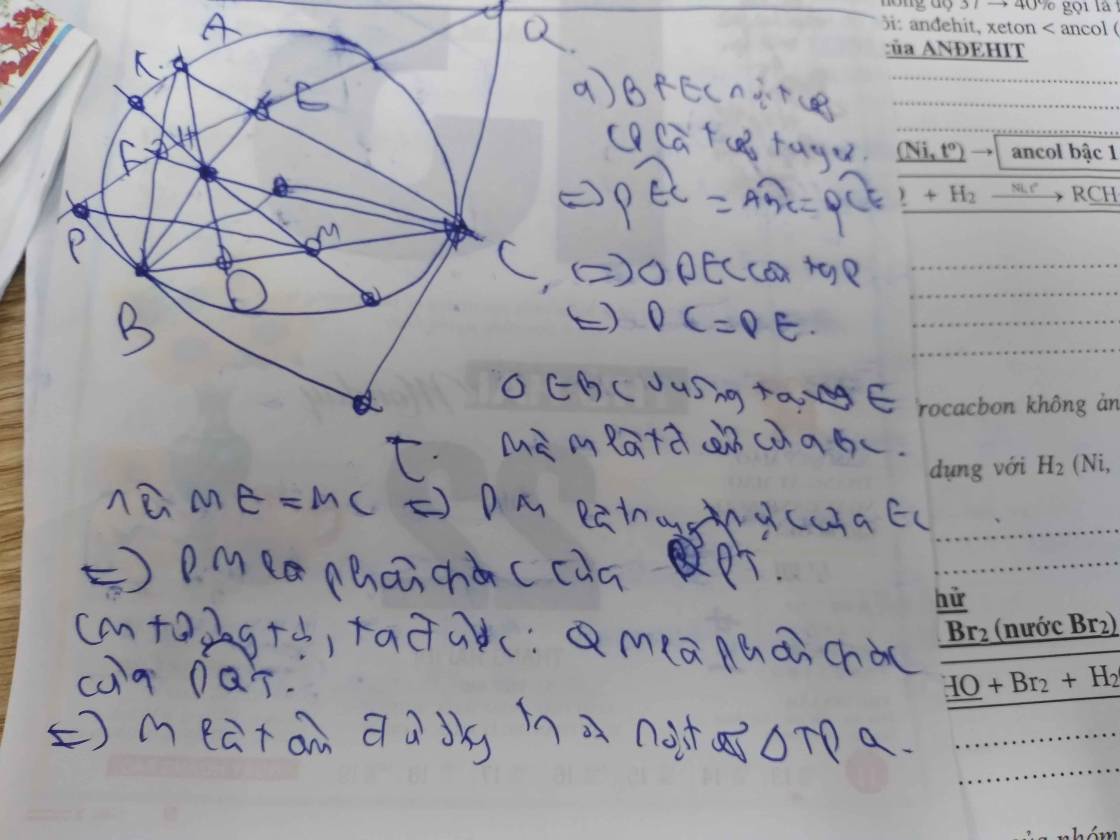
Bài 9: Cho tam giác ABC nội tiếp (O); đường cao AD, BE, CF, trực tâm H, M là trung điểm BC. Gọi AK, AL là tiếp tuyến của (BC). a) Chứng minh: K, H, L thẳng hàng. b) Tiếp tuyến tại B và E của (BC) cắt nhau tại T. Gọi TA cắt (O) tại P. Chúng minh: M, H, P thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì DI = DB (gt) nên tam giác DIB cân tại D
Suy ra: \(\widehat{DIB}=\widehat{DBI}\) => \(\widehat{BAD}+\widehat{ABI}=\widehat{IBC}+\widehat{DBC}\)
Mà AD là phân giác góc BAC nên cung BD = cung CD
Ta có: BAD là góc nội tiếp chắn cung BD
DBC là góc nội tiếp chắn cung CD
Do đó: \(\widehat{BAD}=\widehat{DBC}\Rightarrow\widehat{ABI}=\widehat{IBC}\)
=> BI là phân giác của góc ABC
Lại có: AI là phân giác góc BAC
Vậy I là tâm đường tròn nội tiếp tam giác ABC (Đpcm)

a) Xét tứ giác AEHF có
\(\widehat{HEA}+\widehat{HFA}=180^0\)
nên AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét tứ giác AEDB có
\(\widehat{AEB}=\widehat{ADB}\left(=90^0\right)\)
nên AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

Chọn đáp án C.
Gọi M là trung điểm của BC: 
Do tam giác ABC đều nên tâm đường tròn nội tiếp tam giác ABC là trọng tâm, tâm đường tròn ngoại tiếp tam giác ABC
Áp dụng định lí Pytago vào tam giác ABM ta có:


a. Vì I là trung điểm của AC \(\Rightarrow\) OI \(\perp\) AC ( quan hệ giữa đk và dây )
hay KI \(\perp\) AC
Xét tứ giác CIKH có: góc KIC + góc KHC = 90o + 90o = 180o ( tổng 2 góc đối = 180o )
\(\Rightarrow\) tứ giác CIKH nội tiếp ( đpcm )
b. Ta có: góc CBD = góc CAD ( 2 góc nội tiếp cùng chắn cung DC ) (1)
Xét \(\Delta\) AKC có: KI là đường trung tuyến đồng thời là đường cao
\(\Rightarrow\) \(\Delta\) AKC là tam giác cân tại K \(\Rightarrow\) góc CAK = góc ACK
hay góc CAD = góc ACK (2)
Từ (1), (2) \(\Rightarrow\) góc ACK = góc CBD ( đpcm )