hai giá sách có 270 quyển sách. Nếu chuyển từ giá 1 sang giá 2 10 cuốn thì số sách giá 1 bằng 5/4 số sách giá 2. Tìm số sách mỗi giá lúc đầu.
Giúp mình với ạ, mình cảm ơn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
Gọi số sách ở giá thứ nhất là x ( cuốn)
Số sách ở giá thứ hai là y (cuốn), (x, y∈ N*; x> 50, x< 450, y< 450)
Hai giá sách có tất cả 450 cuốn nên x+ y = 450 (1)
Khi chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách ở giá thứ nhất khi đó là x- 50 và số sách ở giá thứ hai là y+ 50
Theo đầu bài ta có:
Vậy số sách ở giá thứ nhất là 300 quyển, giá thứ hai là 150 quyển.
Chúc em học giỏi

Nếu chuyển 50 cuốn sách từ giá 1 sang giá 2 thì số sách 2 ngăn không đổi.
Gọi số sách ở giá 1 ; giá 2 sau khi chuyển lần lượt là a ; b \(\left(a;b\inℕ^∗\right)\)
Theo bài ta có : \(b=\frac{4}{5}a\)(1)
Lại có : a + b = 450 (2)
Thay (1) vào (2) ta có :
\(a+\frac{4}{5}a=450\)
\(\Rightarrow a\left(1+\frac{4}{5}\right)=450\)
\(\Rightarrow a.\frac{9}{5}=450\)
=> a = 250
=> Số sách ở giá 1 ban đầu là : 250 + 50 = 300 cuốn
=> Số sách ở giá 2 ban đầu là : 450 - 300 = 150 cuốn

Nếu chuyển 15 cuốn sách từ giá thứ nhất sang thứ hai vậy hiệu 2 giá sách là:
15 x 2 = 30 (cuốn)
Giá thứ nhất có số sách là:
(150 + 30) : 2 = 90 (cuốn)
Giá thứ hai có số sách là:
150 - 90 = 60 (cuốn)
Đáp số : Giá thứ nhất : 90 cuốn
Giá thứ hai : 60 cuốn

Gọi số sách ở giá thứ nhất là x ( cuốn)
Số sách ở giá thứ hai là y (cuốn), (x, y∈ N*; x> 50, x< 450, y< 450)
Hai giá sách có tất cả 450 cuốn nên x+ y = 450 (1)
Khi chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách ở giá thứ nhất khi đó là x- 50 và số sách ở giá thứ hai là y+ 50
Theo đầu bài ta có:
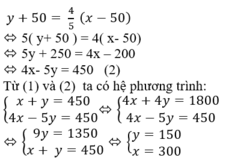
Vậy số sách ở giá thứ nhất là 300 quyển, giá thứ hai là 150 quyển.

Gọi số sách ở giá thứ nhất là x ( cuốn)
Số sách ở giá thứ hai là y (cuốn), (x, y∈ N*; x> 50, x< 450, y< 450)
Hai giá sách có tất cả 450 cuốn nên x+ y = 450 (1)
Khi chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách ở giá thứ nhất khi đó là x- 50 và số sách ở giá thứ hai là y+ 50
Theo đầu bài ta có:
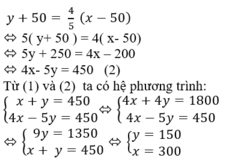
Vậy số sách ở giá thứ nhất là 300 quyển, giá thứ hai là 150 quyển.

Gọi số sách giá 1 là:\(x\)(quyển) điều kiện:\(x\inℕ^∗\)
\(\Rightarrow\)số sách giá 2 là:\(540-x\)(quyển)
\(\Rightarrow\)số sách giá 1 sau khi chuyển là:\(x-60\)(quyển)
\(\Rightarrow\)số sách giá 2 sau khi nhận là:\(540-x+60\)(quyển)
Nếu chuyển 60 cuốn từ giá 1 sang giá 2 thì số sách giá 2 bằng 125% số sách giá 1 nên ta có phương trình:
\(125\%\left(x-60\right)=540-x+60\)
\(\Leftrightarrow\frac{125x}{100}-\frac{125.60}{100}=600-x\)
\(\Leftrightarrow\frac{5x}{4}-75=600-x\)
\(\Leftrightarrow\frac{5}{4}x+x=600+75\)
\(\Leftrightarrow\frac{9}{4}x=675\Leftrightarrow x=300\left(tm\right)\)
Vậy số sách giá 1 là 300 quyển
số sách giá 2 là 540-300=240 quyển
Gọi số sách ở giá 1 là x ( quyển , x thuộc N* và < 540 )
=> Số sách ở giá 2 là 540 - x
Chuyển 60 quyển từ giá 1 sang giá 2 thì giá 2 = 125% = 5/4 giá 1
=> Ta có phương trình : \(\frac{5}{4}\left(x-60\right)=540-x+60\)
<=> \(\frac{5\left(x-60\right)}{4}=\frac{4\left(540-x+60\right)}{4}\)
<=> \(5x-300=2160-4x+240\)
<=> \(5x+4x=2160+240+300\)
<=> \(9x=2700\)
<=> \(x=300\left(tmđk\right)\)
=> Số sách ở giá 1 là 300 quyển
=> Số sách ở giá 2 = 540 - 300 = 240

Gọi số sách ở giá thứ nhất là x
--->số sách ở giá thứ hai là 450 - x
Vậy số sách ở giá thứ nhất sau khi chuyển là x - 50
Vậy số sách ở giá thứ hai sau khi chuyển là 500 - x
Ta có pt
x - 50 = 4/5 * (500 - x )
Giải pt trên x = 250
----> số sách giá 1 là 250 , giá 2 là 200
L - i - k - e nha

Ban đầu giá sách 2 có số cuốn là:
(58 - 7 +3) ;2 = 27 ( cuốn )
Đáp số 57 cuốn
tink mình cấy mình trả lời nhanh nhất
Sau khi chuyển một số sách từ ngăn này sang ngăn kia thì tổng số sách không thay đổi.
Số sách sau khi chuyển của mỗi ngăn là:
58 : 2 = 29 (cuốn)
Ban đầu giá thứ hai cố số quyển sách là:
29 + 3 - 7 = 25 (cuốn)
Đáp số: 25 cuốn sách.

Gọi số sách ban đầu ở giá 1 là x cuốn (\(10< x< 270;x\in N\))
Số sách ban đầu ở giá 2 là: \(270-x\) cuốn
Số sách giá 1 sau khi chuyển 10 cuốn sang giá 2: \(x-10\) cuốn
Số sách giá 2 sau khi chuyển: \(270-x+10=280-x\) cuốn
Do lúc đó số sách giá 1 bằng 5/4 số sách giá 2 nên ta có pt:
\(x-10=\dfrac{5}{4}\left(280-x\right)\)
\(\Leftrightarrow x+\dfrac{5}{4}x=360\)
\(\Leftrightarrow x=160\)
Vậy số sách ban đầu ở giá 1 là 160 cuốn, giá 2 là 110 cuốn