Giải phương trình sau:
x+5/x-5 = 5/x2-5x + 1/x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: (x + 4)(5x – 1) > 5 x 2 + 16x + 2
⇔ 5 x 2 – x + 20x – 4 > 5 x 2 + 16x + 2
⇔ 5 x 2 – x + 20x – 5 x 2 – 16x > 2 + 4
⇔ 3x > 6
⇔ x > 2
Vậy tập nghiệm của bất phương trình là S = {x|x > 2}

a) (x – 1)(x2 + x + 1) – 2x = x(x – 1)(x + 1)
⇔ x3 – 1 – 2x = x(x2 – 1)
⇔ x2 – 1 – 2x = x3 – x
⇔ -2x + x = 1 ⇔ - x = 1 ⇔ x = -1
Tập nghiệm của phương trình: S = { -1}
b) x2 – 3x – 4 = 0
⇔ x2 – 4x + x – 4 = 0 ⇔ x(x – 4) + (x – 4) = 0
⇔ (x – 4)(x + 1) = 0 ⇔ x – 4 = 0 hoặc x + 1 = 0
⇔ x = 4 hoặc x = -1
Tập nghiệm của phương trình: S = {4; -1}
c) ĐKXĐ : x – 1 ≠ 0 và x2 + x + 1 ≠ 0 (khi đó : x3 – 1 = (x – 1)(x2 + x + 1) ≠ 0)
⇔ x ≠ 1
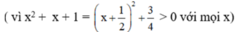
Quy đồng mẫu thức hai vế:
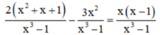
Khử mẫu, ta được: 2x2 + 2x + 2 – 3x2 = x2 – x
⇔ -2x2 + 3x + 2 = 0 ⇔ 2x2 – 3x – 2 = 0
⇔ 2x2 – 4x + x – 2 = 0 ⇔ 2x(x – 2) + (x – 2) = 0
⇔ (x – 2)(2x + 1) = 0 ⇔ x – 2 = 0 hoặc 2x + 1 = 0
⇔ x = 2 hoặc x = -1/2(thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {2 ; -1/2}
d) ĐKXĐ : x – 5 ≠ 0 và x – 1 ≠ 0 (khi đó : x2 – 6x + 5 = (x – 5)(x – 1) ≠ 0)
Quy đồng mẫu thức hai vế :
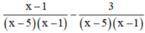
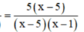
Khử mẫu, ta được : x – 1 – 3 = 5x – 25 ⇔ -4x = -21
⇔ x = 21/4 (thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {21/4}

a) \(\left(3x-2\right)\left(4x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-2=0\\4x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{5}{4}\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{2}{3};-\dfrac{5}{4}\right\}\)
b) \(\left(2,3x-6,9\right)\left(0,1x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2,3x-6,9=0\\0,1x+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-20\end{matrix}\right.\)
c) \(\left(4x+2\right)\left(x^2+1\right)=0\)
Vì \(x^2+1\ge1>0\forall x\)
\(\Rightarrow4x+2=0\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy: \(S=\left\{-\dfrac{1}{2}\right\}\)
d) \(\left(2x+7\right)\left(x-5\right)\left(5x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+7=0\\x-5=0\\5x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{7}{2}\\x=5\\x=-\dfrac{1}{5}\end{matrix}\right.\)
Vậy: \(S=\left\{-\dfrac{7}{2};5;-\dfrac{1}{5}\right\}\)
e) \(\left(x-1\right)\left(2x+7\right)\left(x^2+2\right)=0\)
Vì \(x^2+2\ge2>0\forall x\)
\(\Rightarrow\left(x-1\right)\left(2x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+7=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{7}{2}\end{matrix}\right.\)
f) \(\left(3x+2\right)\left(x^2-1\right)=\left(9x^2-4\right)\left(x+1\right)\)
\(\Leftrightarrow\left(3x+2\right)\left(x-1\right)\left(x+1\right)-\left(3x-2\right)\left(3x+2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[\left(3x+2\right)\left(x+1\right)\right].\left(x-1-3x+2\right)=0\)
\(\Leftrightarrow\left(3x^2+5x+2\right)\left(-2x+1\right)=0\)
\(\Leftrightarrow\left(3x^2+3x+2x+2\right)\left(-2x+1\right)=0\)
\(\Leftrightarrow\left[3x\left(x+1\right)+2\left(x+1\right)\right]\left(-2x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x+2\right)\left(-2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\3x+2=0\\-2x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{2}{3}\\x=\dfrac{1}{2}\end{matrix}\right.\)
Vậy: \(S=\left\{-1;-\dfrac{2}{3};\dfrac{1}{2}\right\}\)

a, \(\left(x^2-5x+7\right)^2-\left(2x-5\right)^2=0\)
\(\Leftrightarrow\left(x^2-5x+7-2x+5\right)\left(x^2-5x+7+2x-5\right)=0\)
\(\Leftrightarrow\left(x^2-7x+12\right)\left(x^2-3x+2\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(x-3\right)\left(x-1\right)\left(x-2\right)=0\Leftrightarrow x=1;x=2;x=3;x=4\)
Vậy tập nghiệm phương trình là S = { 1 ; 2 ; 3 ; 4 }
b, \(\left|2x-1\right|=5\Leftrightarrow\left[{}\begin{matrix}2x-1=5\\2x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)
Vậy tập nghiệm của phương trình là S = { -2 ; 3 }
c, \(\left|2x-1\right|=\left|x+5\right|\Leftrightarrow\left(2x-1\right)^2=\left(x+5\right)^2\)
\(\Leftrightarrow\left(2x-1\right)^2-\left(x+5\right)^2=0\Leftrightarrow\left(2x-1-x-5\right)\left(2x-1+x+5\right)=0\Leftrightarrow x=6;x=-\dfrac{4}{3}\)
Vậy tập nghiệm của phương trình là S = { -4/3 ; 6 }
d, \(\left|3x+1\right|=x-2\)
TH1 : \(3x+1=x-2\Leftrightarrow2x=-3\Leftrightarrow x=-\dfrac{3}{2}\)
TH2 : \(3x+1=-x+2\Leftrightarrow4x=1\Leftrightarrow x=\dfrac{1}{4}\)
Vậy tập nghiệm của phương trình là S = { -3/2 ; 1/4 }
các ý còn lại tương tự
a) Ta có: \(\left(x^2-5x+7\right)^2-\left(2x-5\right)^2=0\)
\(\Leftrightarrow\left(x^2-5x+7-2x+5\right)\left(x^2-5x+7+2x-5\right)=0\)
\(\Leftrightarrow\left(x^2-7x+12\right)\left(x^2-3x+2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-4\right)\left(x-1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-4=0\\x-1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=4\\x=1\\x=2\end{matrix}\right.\)
Vậy: S={3;4;1;2}

Bài 2:
a: =>2x^2-4x+1=x^2+x+5
=>x^2-5x-4=0
=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)
b: =>11x^2-14x-12=3x^2+4x-7
=>8x^2-18x-5=0
=>x=5/2 hoặc x=-1/4

1: \(\Leftrightarrow\left(x-3\right)\left(x+3\right)-\left(x-3\right)\left(5x+2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(-4x+1\right)=0\)
hay \(x\in\left\{3;\dfrac{1}{4}\right\}\)
2: \(\Leftrightarrow\left(x-1\right)\left(x^2+x+1\right)-\left(x-1\right)\left(x^2-2x+16\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+x+1-x^2+2x-16\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(3x-15\right)=0\)
hay \(x\in\left\{1;5\right\}\)
3: \(\Leftrightarrow\left(x-1\right)\left(4x^2-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x-1\right)\left(2x+1\right)=0\)
hay \(x\in\left\{1;\dfrac{1}{2};-\dfrac{1}{2}\right\}\)
4: \(\Leftrightarrow x^2\left(x+4\right)-9\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-3\right)\left(x+3\right)=0\)
hay \(x\in\left\{-4;3;-3\right\}\)
5: \(\Leftrightarrow\left[{}\begin{matrix}3x+5=x-1\\3x+5=1-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=-6\\4x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-1\end{matrix}\right.\)
6: \(\Leftrightarrow\left(6x+3\right)^2-\left(2x-10\right)^2=0\)
\(\Leftrightarrow\left(6x+3-2x+10\right)\left(6x+3+2x-10\right)=0\)
\(\Leftrightarrow\left(4x+13\right)\left(8x-7\right)=0\)
hay \(x\in\left\{-\dfrac{13}{4};\dfrac{7}{8}\right\}\)
1.
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)=\left(x-3\right)\left(5x-2\right)\)
\(\Leftrightarrow x+3=5x-2\)
\(\Leftrightarrow4x=5\Leftrightarrow x=\dfrac{5}{4}\)
2.
\(\Leftrightarrow\left(x-1\right)\left(x^2+x+1\right)=\left(x-1\right)\left(x^2-2x+16\right)\)
\(\Leftrightarrow x^2+x+1=x^2-2x+16\)
\(\Leftrightarrow3x=15\Leftrightarrow x=5\)
3.
\(\Leftrightarrow4x^2\left(x-1\right)-\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(4x^2-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{2};x=-\dfrac{1}{2}\end{matrix}\right.\)
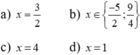

\(\dfrac{x+5}{x-5}=\dfrac{5}{x^2-5x}+\dfrac{1}{x}\)
\(\Leftrightarrow\dfrac{x+5}{x-5}=\dfrac{5}{x\left(x-5\right)}+\dfrac{1}{x}\)
ĐKXĐ : \(\left\{{}\begin{matrix}x\ne0\\x-5\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne0\\x\ne5\end{matrix}\right.\)
Ta có : \(\dfrac{x+5}{x-5}=\dfrac{5}{x\left(x-5\right)}+\dfrac{1}{x}\)
\(\Leftrightarrow\dfrac{x\left(x+5\right)}{x\left(x-5\right)}=\dfrac{5}{x\left(x-5\right)}+\dfrac{x-5}{x\left(x-5\right)}\)
`=> x (x+5) = 5 +x-5`
`<=> x^2 +5x - 5-x+5=0`
`<=> x^2 +4x =0`
`<=> x(x+4)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(l\right)\\x=-4\end{matrix}\right.\)
Vậy phương trình có nghiệm `x=-4`