1 lon sữa có dạng hình trụ với bán kính đáy 3,5 cm và chiều cao 7,8.Tính thể tích sữa chứa trong lon
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 4 2023
Gọi chiều cao là x
=>Bán kính là 0,4x
Theo đề, ta có; x*(0,4x)^2*pi=540*pi
=>0,16*x^3=540
=>x=15
=>Bán kính là 6cm
Diện tích vỏ hộp là:
2*pi*15*6+2*pi*15^2
=630pi(cm2)
NM
Nguyễn Minh Quang
Giáo viên
1 tháng 6 2021
Gọi R là bán kính đáy hộp sữa
\(\Rightarrow\)chiều cao hộp sữa là : \(3R\)
Thể tích hộp sữa là : \(\pi R^2\times3R=192\pi\Leftrightarrow R^3=64\Leftrightarrow R=4cm\)
Ơ mà sao lại hỏi thể tích nhỉ, đề cho luôn là \(192\pi cm^3\) mà nhỉ
11 tháng 5 2021
Đáp án: 28,1
Giải thích các bước giải:
a) Đường kính đáy của hình nón đó là:
d = 2 . r = 2 . 2 = 4
Vì chiều cao của hình nón đó bằng đường kính đáy của hình nón đó nên chiều cao h của hình nón đó là: h = 4 (cm)
Ta có: l² = r² + h² (theo định lý Py - ta - go)
⇒ l = √(r² + h²) = √(2² + 4²) = √(4 + 16) = √20 (cm)
Diện tích xung quanh của hình nón đó là: Sxq = π . r . l = π . 2 . √20 ≈ 28,1(cm²)
Vậy diện tích xung quanh của hình nón đó là ≈ 28,1
CM
21 tháng 1 2017
Chọn đáp án A.
Gọi r, h lần lượt là bán kính đáy và chiều cao của lon sữa bò cần thiết kế.
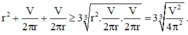
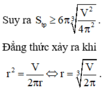
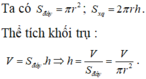
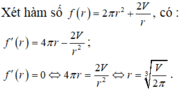
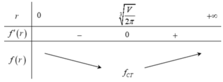
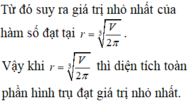
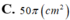
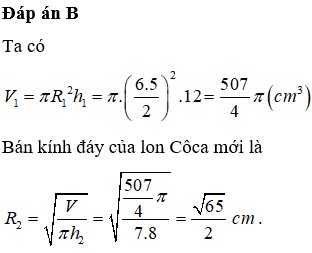
Ờ .......... khoảng 300 đúng hông . sai đừng nói gì mình nghe
Thể tích sữa chứa trong lon:
\(V=\pi r^2h=3,5^2.7,8.\dfrac{22}{7}=300,3\left(cm^3\right)=300,3\left(ml\right)\)