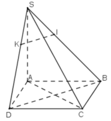
Cho hình chóp S.ABCD có đáy là hình vuông tâm O, cạnh bằng a. SA LOABCD) và SA= a a) Chứng minh BD L(SAC) và CD L(SAD). b) Gọi điểm 1 là trung điểm của đoạn SD. Tính độ dài các đoạn thẳng SD và KC . c) Tìm hinh chiếu của đường thẳng KC lên mặt phẳng (ABCD). Tính góc giữa C và (ABCD).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 4 2022
Có : AC vuông góc với BD (hình vuông ABCD)
SA vuông góc với BD ( do SA vuông góc với mp ABCD)
=> BD vuông góc với mp SAC...
22 tháng 2 2021
.png)
+ SA⊥(ABCD)⇒SA⊥BDSA⊥(ABCD)⇒SA⊥BD (1)
+ ABCD là hình vuông ⇒AC⊥BD⇒AC⊥BD (2)
+ Từ (1) và (2) suy ra BD⊥(SAC)⇒BD⊥SCBD⊥(SAC)⇒BD⊥SC
19 tháng 4 2023
a: CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
b: (SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=1/2
=>góc SDA=27 độ
22 tháng 4 2023
1: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
BD vuông góc CA
BD vuông góc SA
=>BD vuông góc (SAC)
2: DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SCD) vuông góc (SAD)
4: (SC;(SAB))=(SC;SB)=góc CSB
\(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(SC=\sqrt{AC^2+SA^2}=a\sqrt{5}\)
\(SB=\sqrt{SA^2+AB^2}=2a\)
BC=a
Vì SB^2+BC^2=SC^2
nên ΔSCB vuông tại B
sin CSB=BC/SC=1/căn 5
=>góc CSB=27 độ
3: BC vuông góc SAB
=>AE vuông góc BC
mà AE vuông góc SB
nên AE vuông góc (SBC)
=>AE vuông góc SC
4: (SB;(SAC))=(SB;SD)=góc DSB
\(SD=\sqrt{SA^2+AD^2}=2a;SB=2a;DB=a\sqrt{2}\)
\(cosDSB=\dfrac{4a^2+4a^2-2a^2}{2\cdot2a\cdot2a}=\dfrac{3}{4}\)
=>góc DSB=41 độ
10 tháng 5 2023
a: DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
b: (SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=căn 3
=>góc SDA=60 độ
a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
CD vuông góc SA
CD vuông góc AD
=>CD vuông góc (SAD)
b: \(SD=\sqrt{a^2+a^2}=a\sqrt{2}\)