 Giúp mình 2 câu này
Giúp mình 2 câu này
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


cái này trong SGK thì tra google thì nhanh hơn đó bạn *ý kiến riêng*
Chúc bạn học tốt! :3

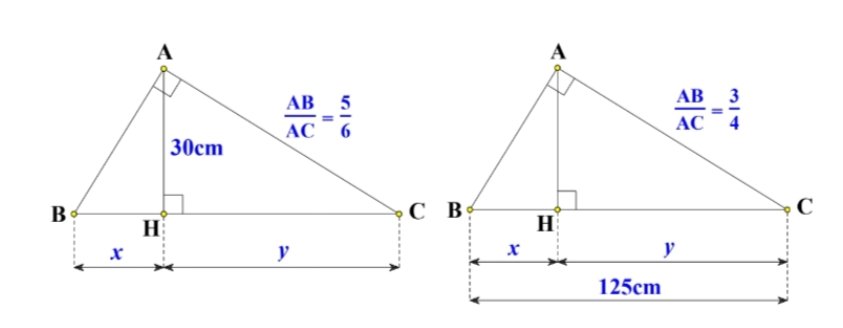
a: AB/AC=5/6
=>HB/HC=25/36
=>HB/25=HC/36=k
=>HB=25k; HC=36k
AH^2=HB*HC
=>25k*36k=30^2
=>900k^2=900
=>k=1
=>x=25cm; y=25cm
b: AB/AC=3/4
=>HB/HC=9/16
=>x/y=9/16
=>x/9=y/16=(x+y)/(9+16)=125/25=5
=>x=45cm; y=80cm


b.
\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt{x^2+3x-1}+x\right)=\lim\limits_{x\rightarrow-\infty}\left(\dfrac{3x-1}{\sqrt{x^2+3x-1}-x}\right)\)
\(=\lim\limits_{x\rightarrow-\infty}\left(\dfrac{3-\dfrac{1}{x}}{-\sqrt{1+\dfrac{3}{x}-\dfrac{1}{x^2}}-1}\right)=\dfrac{3-0}{-1-1}=-\dfrac{3}{2}\)
d.
\(\lim\limits_{x\rightarrow-\infty}\dfrac{2x^2+3x}{\sqrt{4x^4+2x^2}+3x^2-1}=\lim\limits_{x\rightarrow-\infty}\dfrac{2+\dfrac{3}{x}}{\sqrt{4+\dfrac{2}{x^2}}+3-\dfrac{1}{x^2}}\)
\(=\dfrac{2+0}{\sqrt{4+0}+3-0}=\dfrac{2}{5}\)

7:
a: \(P=\left(1:\dfrac{x-x+1}{\sqrt{x}+\sqrt{x-1}}-\dfrac{x-1-2}{\sqrt{x-1}-\sqrt{2}}\right)\cdot\left(\dfrac{2\sqrt{x}-\sqrt{x}-\sqrt{2}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}\right)\)\(=\left(\sqrt{x}+\sqrt{x-1}-\sqrt{x-1}-\sqrt{2}\right)\cdot\dfrac{\sqrt{x}-\sqrt{2}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}\)
\(=-\dfrac{\left(\sqrt{x}-\sqrt{2}\right)}{\sqrt{x}}\)
b: Khi x=3-2căn 2 thì \(P=-\dfrac{\sqrt{2}-1-\sqrt{2}}{\sqrt{2}-1}=\dfrac{1}{\sqrt{2}-1}=\sqrt{2}+1\)





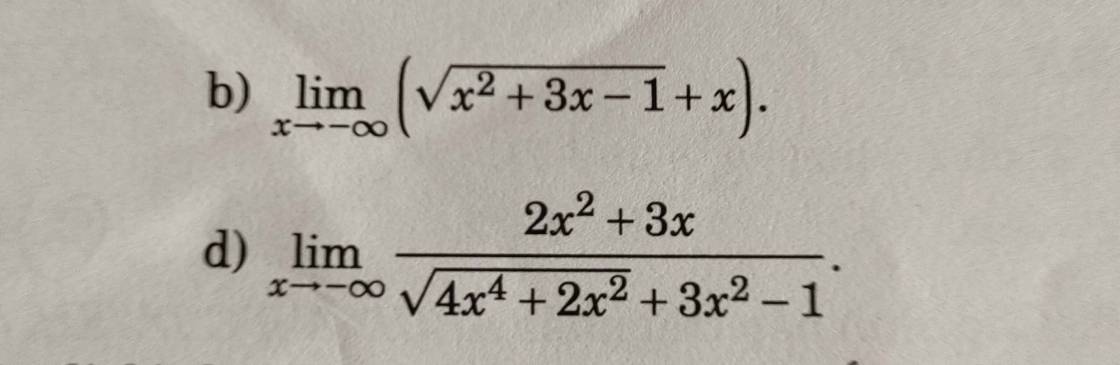
 Giúp mình giải 2 câu này với. Mình cảm ơn
Giúp mình giải 2 câu này với. Mình cảm ơn

a.
\(\lim\left(\sqrt[3]{n^3+2}-\sqrt[]{n^2+n}\right)=\lim\left(\sqrt[3]{n^3+2}-n+n-\sqrt[]{n^2+n}\right)\)
\(=\lim\left(\dfrac{2}{\sqrt[3]{\left(n^3+2\right)^2}+n\sqrt[3]{n^3+n}+n^2}-\dfrac{n}{n+\sqrt[]{n^2+n}}\right)\)
\(=\lim\left(\dfrac{2}{\sqrt[3]{\left(n^3+2\right)^2}+n\sqrt[3]{n^3+2}+n^2}-\dfrac{1}{1+\sqrt[]{1+\dfrac{1}{n}}}\right)\)
\(=0-\dfrac{1}{1+1}=-\dfrac{1}{2}\)
b.
\(\lim\limits_{x\rightarrow2}\dfrac{\sqrt[]{x+2}+\sqrt[]{3x-2}-2x}{x-2}=\lim\limits_{x\rightarrow2}\dfrac{\sqrt[]{x+2}-2+\sqrt[]{3x-2}-2-2x+4}{x-2}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{x-2}{\sqrt[]{x+2}+2}+\dfrac{3\left(x-2\right)}{\sqrt[]{3x-2}+2}-2\left(x-2\right)}{x-2}\)
\(=\lim\limits_{x\rightarrow2}\left(\dfrac{1}{\sqrt[]{x+2}+2}+\dfrac{3}{\sqrt[]{3x-2}+2}-2\right)=-1\)