Cho hình thang ABCD (AB//CD), AB=5cm, CD=13cm. Một đường thẳng d song song với các đáy hình thang, cắt các cạnh AD, BC lần lượt tại E và F. Tính độ dài EF để SABFE = \(\frac{1}{6}\)SABCD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tam giác ABD có:
AB//IE (gt)
=>\(\dfrac{IE}{AB}=\dfrac{DI}{BD}\)(định lí Ta-let). (1)
Xét tam giác ABI có:
AB//DC (gt)
=>\(\dfrac{DI}{BD}=\dfrac{CI}{AC}\)(định lí Ta-let) (2)
Xét tam giác ABC có:
IF//AB (gt)
=>\(\dfrac{IF}{AB}=\dfrac{CI}{AC}\)(định lí Ta-let) (3)
- Từ (1),(2),(3) suy ra \(\dfrac{EI}{AB}=\dfrac{IF}{AB}\)=>EI=IF
Ta có: \(\dfrac{IE}{AB}=\dfrac{DI}{BD}\)(cmt) =>\(\dfrac{AB}{IE}=\dfrac{BD}{DI}\)=>\(\dfrac{AB}{IE}-1=\dfrac{BI}{DI}\)(4)
Xét tam giác ABI có:
AB//DC (gt)
=>\(\dfrac{BI}{DI}=\dfrac{AB}{DC}\)(định lí Ta-let) (5)
- Từ (4) và (5) suy ra: \(\dfrac{AB}{IE}-1=\dfrac{AB}{DC}\)
=>\(\dfrac{AB}{IE}=\dfrac{DC+AB}{DC}\)
=>IE=IF=\(\dfrac{AB.DC}{AB+DC}=\dfrac{4.5}{9}=\dfrac{20}{9}\left(cm\right)\)

gọi giao điểm của AC và EF là O
có EO//CD(EF//CD;O\(\in\)EF)
=>\(\frac{AE}{AD}=\frac{EO}{CD}\)(hệ quả ta-lét)
=>\(\frac{1}{3}=\frac{EO}{4}\left(CD=4cm;\frac{AE}{AD}=\frac{1}{3}\right)\)
=> EO=\(\frac{4}{3}\)cm
có BF=\(\frac{1}{3}\)BC(gt)=>CF=(1-\(\frac{1}{3}\))BC=\(\frac{2}{3}\)BC
Có FO//AB(EF//CD;O\(\in\)EF)
=>\(\frac{CF}{CB}=\frac{FO}{AB}\)(hệ quả talet)
=>\(\frac{2}{3}=\frac{FO}{1}\left(\frac{CF}{CB}=\frac{2}{3};AB=1cm\right)\)
=>FO=\(\frac{2}{3}\)cm
Có EO+FO=EF(O\(\in\)EF)
=>EF=\(\frac{4}{3}\)+\(\frac{2}{3}\)=\(\frac{6}{3}\)=2cm
vậy độ dài EF=2cm

Em tham khảo nha.
Coi AB = 1, DC = k thì \(\frac{DO}{OB}=\frac{DC}{AB}=k\Rightarrow\frac{DO}{DB}=\frac{k}{k+1}\)
\(\Rightarrow OE=OF=\frac{k}{k+1}\Rightarrow EF=\frac{2k}{k+1}\)
Ta có \(\frac{1}{AB}+\frac{1}{CD}=\frac{1}{1}+\frac{1}{k}=\frac{k+1}{k}\)
\(\frac{2}{EF}=\frac{2}{\frac{2k}{k+1}}=\frac{k+1}{k}\)
Vậy nên \(\frac{1}{AB}+\frac{1}{CD}=\frac{2}{EF}\)
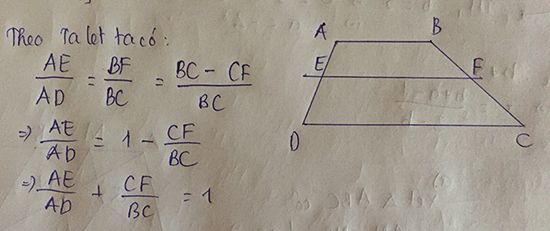 Đây nha !!
Đây nha !!
tk ủng hộ nha mina