Tìm số tự nhiên n biết rằng
2.22+3.22+...+n.2n=2n+10
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NP
0
S
29 tháng 11 2021
2n+10 chia hết cho n+3
=) 2n+6 + 4 chia hết cho n+3
=) 2(n+3) + 4 chia hết cho n+3
=) 4 chia hết cho n+3
=) n+3 thuộc Ư(4)={1; 2; 4}
mà n thuộc N
=> n = 1
HH
1
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 5 2021
Ủa dấu thứ 2 là + hay trừ bạn? Là dấu trừ đúng ko?
Xét khai triển:
\(\left(-1+x\right)^{2n+1}=-C_{2021}^0+C_{2021}^1x-C_{2021}^2x^2+...+C_{2021}^{2021}x^{2021}\)
Đạo hàm 2 vế:
\(\left(2n+1\right)\left(-1+x\right)^{2n}=C_{2021}^1-2xC_{2021}^2+3x^2C_{2021}^3-...+\left(2n+1\right)x^{2n}C_{2021}^{2021}\)
Thay \(x=2\) ta được:
\(2n+1=C_{2021}^1-2.2C_{2021}^2+3.2^2C_{2021}^3-...+\left(2n+1\right)2^{2n}C_{2021}^{2021}\)
\(\Rightarrow2n+1=2005\)
\(\Rightarrow n=1002\)
8 tháng 11 2023
Bài 1: Gọi d=ƯCLN(3n+11;3n+2)
=>\(\left\{{}\begin{matrix}3n+11⋮d\\3n+2⋮d\end{matrix}\right.\)
=>\(3n+11-3n-2⋮d\)
=>\(9⋮d\)
=>\(d\in\left\{1;3;9\right\}\)
mà 3n+2 không chia hết cho 3
nên d=1
=>3n+11 và 3n+2 là hai số nguyên tố cùng nhau
Bài 2:
a:Sửa đề: \(n+15⋮n-6\)
=>\(n-6+21⋮n-6\)
=>\(n-6\in\left\{1;-1;3;-3;7;-7;21;-21\right\}\)
=>\(n\in\left\{7;5;9;3;13;3;27;-15\right\}\)
mà n>=0
nên \(n\in\left\{7;5;9;3;13;3;27\right\}\)
b: \(2n+15⋮2n+3\)
=>\(2n+3+12⋮2n+3\)
=>\(12⋮2n+3\)
=>\(2n+3\in\left\{1;-1;2;-2;3;-3;4;-4;6;-6;12;-12\right\}\)
=>\(n\in\left\{-1;-2;-\dfrac{1}{2};-\dfrac{5}{2};0;-3;\dfrac{1}{2};-\dfrac{7}{2};\dfrac{3}{2};-\dfrac{9}{12};\dfrac{9}{2};-\dfrac{15}{2}\right\}\)
mà n là số tự nhiên
nên n=0
c: \(6n+9⋮2n+1\)
=>\(6n+3+6⋮2n+1\)
=>\(2n+1\inƯ\left(6\right)\)
=>\(2n+1\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
=>\(n\in\left\{0;-1;\dfrac{1}{2};-\dfrac{3}{2};1;-2;\dfrac{5}{2};-\dfrac{7}{2}\right\}\)
mà n là số tự nhiên
nên \(n\in\left\{0;1\right\}\)
DU
2
15 tháng 1 2022
\(\Leftrightarrow2n+2\in\left\{2;4;8\right\}\)
hay \(n\in\left\{0;1;3\right\}\)
TL
1
30 tháng 1 2023
Ta thấy dãy số trên cách đều nhau 2 đơn vị nên ta có số số hạng là:
\(\left[\left(2n-1\right)-1\right]:2+1=n\) ( số )
Tổng dãy số trên sẽ là: \(\left(2n-1+1\right).n\div2=n^2\)
Mà dãy số trên bằng 225 => \(n^2=225\)
=> n = \(\sqrt{225}=15\)
Vậy số tự nhiên cần tìm là n = 15
3 tháng 11 2018
Gọi d là UCLN của 7n + 10 và 5n + 7
Khi đó : 7n + 10 chia hết cho d , 5n + 7 chia hết cho d
<=> 5(7n + 10) chia hết cho d , 7(5n + 7) chia hết cho d
<=> 35n + 50 chia hết cho d , 35n + 49 chia hết cho d
<=> (35n + 50) - (35n + 49) chia hết cho d
<=> 35n + 50 - 35n - 49 chia hết cho d
<=> 1 chia hết cho d
=> d là ư(1)
=> d = 1
Vậy đpcm
CM
8 tháng 2 2018
Chọn A.
Phương pháp:
Áp dụng công thức khai triển nhị thức Newton:
LQ
2
XO
30 tháng 11 2019
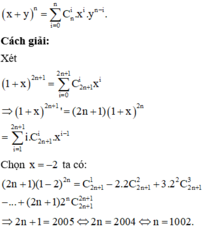
Để \(2n+18⋮2n+5\)
\(\Rightarrow2n+5+13⋮2n+5\)
Vi \(2n+5⋮2n+5\)
\(\Rightarrow13⋮2n+5\)
\(\Rightarrow2n+5\inƯ\left(13\right)\)
\(\Rightarrow2n+5\in\left\{1;13\right\}\)
\(\Rightarrow n\in\left\{-2;4\right\}\)
=> n = 4
Vậy n = 4
30 tháng 11 2019
\(\left(2n+18\right)⋮\left(2n+5\right)\Leftrightarrow\frac{2n+18}{2n+5}=1+\frac{13}{2n+5}\in N\Leftrightarrow\frac{13}{2n+5}\in N\)
\(\Leftrightarrow2n+5\inƯ\left(13\right)=\left\{1;13\right\}\Leftrightarrow n\in\left\{-2;4\right\}\)
mà do \(n\in N\)nên n=4
Đặt A = 2.22 + 3.23 +...+ n.2n
2A = 2.23 + 3.24 +...+ n.2n+1
2A - A = (2.23 - 3.23) + (3.24 - 4.24) +...+ [(n - 1).2n - n.2n ] + n.2n+1
A = -23 - 24 -...- 2n + n.2n+1 - 2.22
A = n.2n+1 - (23 + 24 +...+ 2n) - 23
Đặt B = 23 + 24 +...+ 2n
2B = 24 + 25 +...+ 2n+1
2B - B = (24 + 25 +...+ 2n+1) - (23 + 24 +...+ 2n)
B = 2n+1 - 23
=> A = n.2n+1 - B - 23
=> A = n.2n+1 - (2n+1 - 23) - 23
=> A = n.2n+1 - 2n+1 + 23 - 23
=> A = 2n+1.(n - 1)
Thay A vào ta được:
2n+1.(n - 1) = 2n+10
n - 1 = 2n+10 : 2n+1
n - 1 = 29
n - 1 = 512
n = 512 + 1
n = 513