Cho tam giác HIK có HI=HK.Gọi M là trung điểm của IK.Chứng minh tam giác HIM=tam giác HKM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
V
2
30 tháng 3 2023
`\text {Xét Tam giác HIK: HI = HK}`
`-> \text {Tam giác HIK cân tại H}`
`->`\(\widehat{I}=\widehat{K}\)
Xét Tam giác `HIM` và Tam giác `HKM` có:
`HI = HK (g``t)`
\(\widehat{I}=\widehat{K} (\text {CMT})\)
`MI = MK (\text {M là trung điểm của IK})`
`=> \text {Tam giác HIM = Tam giác HKM (c-g-c)}`
29 tháng 12 2021
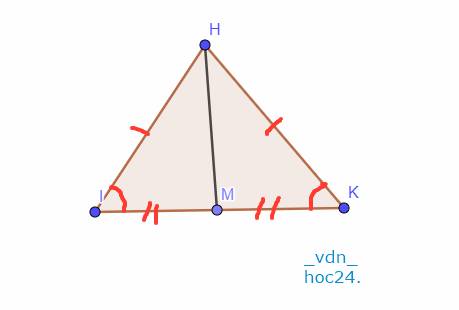
b: Xét ΔHIM và ΔHKM có
HI=HK
HM chung
IM=KM
Do đó: ΔHIM=ΔHKM
4 tháng 3 2022
a: Xét ΔHIK có IN là phân giác
nên HN/NK=HI/IK=HK/IK(1)
Xét ΔHIK có KM là phân giác
nên HM/MI=HK/KI(2)
Từ (1) và (2) suy ra HN/NK=HM/MI
=>MN//IK
=>ΔHMN\(\sim\)ΔHIK
b: Ta có: HN/HI=NK/IK
=>HN/10=NK/8
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{HN}{5}=\dfrac{NK}{4}=\dfrac{HN+NK}{5+4}=\dfrac{10}{9}\)
Do đó: HN=50/9(cm)
Xét ΔHIK có MN//IK
nên MN/IK=HN/HK
\(\Leftrightarrow MN=\dfrac{50}{9}:10\cdot8=\dfrac{40}{9}\left(cm\right)\)
14 tháng 5 2022
a: HK=12cm
b: Xét ΔIHM vuông tại H và ΔIEM vuông tại E có
IM chung
\(\widehat{HIM}=\widehat{EIM}\)
Do đó:ΔIHM=ΔIEM
c: Ta có: ΔIHM=ΔIEM
nên IH=IE; MH=ME
=>IM là đường trung trực của EH
14 tháng 5 2022
a, Xét Δ IHK vuông tại H, có :
\(IK^2=IH^2+HK^2\) (định lí Py - ta - go)
=> \(13^2=5^2+HK^2\)
=> \(HK^2=144\)
=> HK = 12 (cm)
b, Xét Δ HIM và Δ EIM, có :
\(\widehat{HIM}=\widehat{EIM}\) (IM là tia phân giác \(\widehat{HIE}\))
IM là cạnh chung
\(\widehat{IHM}=\widehat{IEM}=90^o\)
=> Δ HIM = Δ EIM (g.c.g)
c, Ta có : Δ HIM = Δ EIM (cmt)
=> HI = EI
=> Δ HIE cân tại I
Ta có :
Δ HIE cân tại I
IM là tia phân giác \(\widehat{HIE}\)
=> IM ⊥ EH
10 tháng 5 2022
a: Xét ΔIHM vuông tại H và ΔINM vuông tại N có
IM chung
\(\widehat{HIM}=\widehat{NIM}\)
Do đó: ΔIHM=ΔINM
b: ta có: ΔIHM=ΔINM
nên HM=NM
c: Ta có: HM=MN
mà MN<MK
nên HM<MK
2 tháng 2 2020
Gọi G là trung điểm BC
Ta có:
góc HGM=180-góc HGB-góc MGC=180-góc ACB-DBC=120+DAC=góc HAK(do góc BAD=góc CAE=60 độ)
Mặt khác:
áp dụng t/c đường trung bình ta có:
GM=1/2BD=1/2AB=AH
GH=1/2AC=1/2AE=AK
=>tam giác HAK=tam giác MGH(c.g.c)
=>HK=HM(1)
Tương tự gọi J là trung điểm AC
Ta cũng suy ra được MK=HM(theo tam giác bằng nhau)(2)
=> Từ (1)(2) => Tam giác HKM là tam giác đều
11 tháng 7 2023
a: Xét ΔHIK và ΔHNM có
HI/HN=HK/HM=5/2
góc H chung
=>ΔHIK đồng dạng với ΔHNM
b:
ΔHIK đồng dạng với ΔHNM
=>IK/NM=5/2
=>10/NM=5/2
=>NM=4cm
c: Xét ΔHIK và ΔHAI có
góc HIK=góc HAI(=góc HNM)
góc Hchung
=>ΔHIK đồng dạng với ΔHAI
Vì Tam giác `HIK` có `HI = HK`
`-> \text {Tam giác HIK cân tại H} ->`\(\widehat{I}=\widehat{K}\)
Xét Tam giác `HIM` và Tam giác `HKM` có:
`HI=HK (g``t)`
\(\widehat{I}=\widehat{K}\) `(CMT)`
`MI=MK (` vì `M` là trung điểm của `IK)`
`=> \text {Tam giác HIM = Tam giác HKM (c-g-c)}`
Chứng minh vì sao MI=MK nx nha m, đề chỉ cho là M là trung điểm của IK thôi nên kh thể vt đây là gt đc :v