B1.Giải phương trình
A. x+2/2 = x^2 + 5x+4/x^2+2x + x/x+2
B2. Mẫu số của một phân số lớn hơn tử số của nó là 5. Nếu tăng cả tử và mẫu của nó thêm 5 đơn vị thì đc phân số mới bằng phân số 2/3. Tìm phân số ban đầu.
B3 Cho hình chữ nhật abcd, vẽ ah vuông góc với db (h thuộc db)
A. Cmr tam giác AHB đồng dạng BCD
b. Cm AD^2 = DH.DB
c. Tính độ dài DH, AH biết AB = 12cm, BC = 9cm



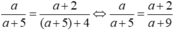
Giúp mình với nhé :)))
Mình làm câu hình thôi. Hôm qua đang làm thì máy sập và..
(Hình xấu quá, sorry)
a/ Xét \(\Delta AHB\)và \(\Delta BCD\)có:
\(\widehat{AHB}=\widehat{BCD}=90^0\left(gt\right)\)
\(\widehat{ABH}=\widehat{BDC}\)(Vì AB//DC, tính chất hình chữ nhật, so le trong)
\(\Rightarrow\Delta ABH~\Delta BDC\left(g.g\right)\)
b/ Xét \(\Delta AHD\)và \(\Delta ADB\)có:
\(\widehat{AHD}=\widehat{DAB}=90^0\left(gt\right)\)
\(\widehat{ADB}:chung\)
\(\Rightarrow\Delta ADH~\Delta BDA\left(g.g\right)\)
\(\Rightarrow\frac{AD}{DB}=\frac{DH}{AD}\)
\(\Rightarrow AD.AD=DH.DB\)
\(\Rightarrow AD^2=DH.DB\)
c/ Ta có: \(BC=AD=9\left(cm\right)\)(tính chất hình chữ nhật)
Xét \(\Delta ABD\)vuông tại \(A\)có:
\(AD^2+AB^2=BD^2\left(pytago\right)\)
\(9^2+12^2=BD^2\)
\(81+144=BD^2\)
\(225=BD^2\)
\(\Rightarrow BD=\sqrt{225}=15\left(cm\right)\)
Ta có: \(\frac{AD}{DB}=\frac{DH}{AD}\left(cmt\right)\Leftrightarrow\frac{9}{15}=\frac{DH}{9}\Rightarrow DH=\frac{9.9}{15}=5,4\left(cm\right)\)
Ta lại có: \(AH=BD-DH=15-5,4=9,6\left(cm\right)\)