 Giúp mình câu 21 22
Giúp mình câu 21 22
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 21:
\(\dfrac{V_{CO_2}}{V_{H_2O}}=\dfrac{4}{3}\Rightarrow\dfrac{n_{CO_2}}{n_{H_2O}}=\dfrac{4}{3}\)
Chọn nCO2 = 4 (mol), nH2O = 3 (mol)
⇒ nZ = 4 - 3 = 1 (mol)
Gọi CTPT của Z là CnH2n-2
\(\Rightarrow n=\dfrac{n_{CO_2}}{n_Z}=4\)
Vậy: CTPT của Z là C4H6.
→ Đáp án: C
Câu 22:
Ta có: nCO2 - nH2O = 1,95 - 1,69 = 0,26 (mol) = nankin
⇒ nanken = 0,78 - 0,26 = 0,52 (mol)
Có: nBr2 = nanken + 2nankin = 1,04 (mol)
\(\Rightarrow m_{Br_2}=1,04.160=166,4\left(g\right)\)
→ Đáp án: B

Câu 21:
Theo ĐLBT KL, có: manken + mBr2 = m sp
⇒ mBr2 = 4,32 - 1,12 = 3,2 (g)
\(\Rightarrow n_{Br_2}=\dfrac{3,2}{160}=0,02\left(mol\right)=n_{anken}\)
Gọi CTPT của anken là CnH2n.
Có: \(M_{anken}=\dfrac{1,12}{0,02}=56\left(g/mol\right)\)
⇒ 12n + 2n = 56 ⇒ n = 4
Vậy: CTPT của anken là C4H8.
→ Đáp án: D
Câu 22:
Gọi CTPT của X là CnH2n.
Ta có: \(30n_{C_2H_6}+n_X.14n=14,6\left(1\right)\)
m bình tăng = mX = 5,6 (g) = nX.14n (2)
Từ (1) và (2) ⇒ nC2H6 = 0,3 (mol)
Có: \(\dfrac{V_X}{V_X+V_{C_2H_6}}=\dfrac{2}{5}\Rightarrow\dfrac{n_X}{n_X+0,3}=\dfrac{2}{5}\Rightarrow n_X=0,2\left(mol\right)\)
Thay vào (2) ta được n = 2
Vậy: CTPT của X là C2H4.
→ Đáp án: B

Câu 21:
\(C_nH_{2n-2}+AgNO_3+NH_3\rightarrow C_nH_{2n-3}Ag+NH_4NO_3\\ n_X=\dfrac{14-5,44}{108-1}=0,08\left(mol\right)=n_{kết.tủa}\\ M_{C_nH_{2n-3}Ag}=\dfrac{14}{0,08}=175\left(\dfrac{g}{mol}\right)=14n+107\\ \Leftrightarrow n=5\\ \Rightarrow CTPT.X:C_5H_8\\ CTCT:CH\equiv C-CH_2-CH_2-CH_3\\ CH_3-C\equiv C-CH_2-CH_3\\ CH\equiv C-CH\left(CH_3\right)-CH_3\)
Chọn C
Câu 22:
\(n_{C_2H_2}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\\ C_2H_2+2Br_2\rightarrow C_2H_2Br_4\\ n_{Br_2}=2.n_{C_2H_2}=2.0,1=0,2\left(mol\right)\\ m_{Br_2}=0,2.160=32\left(g\right)\\ Chọn.A\)

21.
\(\left\{{}\begin{matrix}SA\perp AB\\AC\perp AB\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAC\right)\)
E là trung điểm SA, F là trung điểm SB \(\Rightarrow\) EF là đường trung bình tam giác SAB
\(\Rightarrow EF||AB\Rightarrow EF\perp\left(SAC\right)\)
\(\Rightarrow EF=d\left(F;\left(SEK\right)\right)\)
\(SE=\dfrac{1}{2}SA=\dfrac{3a}{2}\) ; \(EF=\dfrac{1}{2}AB=a\)
\(SC=\sqrt{SA^2+AC^2}=a\sqrt{13}\Rightarrow SK=\dfrac{2}{3}SC=\dfrac{2a\sqrt{13}}{3}\)
\(\Rightarrow S_{SEK}=\dfrac{1}{2}SE.SK.sin\widehat{ASC}=\dfrac{1}{2}.\dfrac{3a}{2}.\dfrac{2a\sqrt{13}}{3}.\dfrac{2a}{a\sqrt{13}}=a^2\)
\(\Rightarrow V_{S.EFK}=\dfrac{1}{3}EF.S_{SEK}=\dfrac{1}{3}.a.a^2=\dfrac{a^3}{3}\)
\(AB\perp\left(SAC\right)\Rightarrow AB\perp\left(SEK\right)\Rightarrow AB=d\left(B;\left(SEK\right)\right)\)
\(\Rightarrow V_{S.EBK}=\dfrac{1}{3}AB.S_{SEK}=\dfrac{1}{3}.2a.a^2=\dfrac{2a^3}{3}\)
22.
Gọi D là trung điểm AB
Do tam giác ABC đều \(\Rightarrow CD\perp AB\Rightarrow CD\perp\left(SAB\right)\)
\(\Rightarrow CD=d\left(C;\left(SAB\right)\right)\)
\(CD=\dfrac{AB\sqrt{3}}{2}=a\sqrt{3}\) (trung tuyến tam giác đều)
N là trung điểm SC \(\Rightarrow d\left(N;\left(SAB\right)\right)=\dfrac{1}{2}d\left(C;\left(SAB\right)\right)=\dfrac{a\sqrt{3}}{2}\)
\(S_{SAB}=\dfrac{1}{2}SA.AB=a^2\sqrt{3}\) \(\Rightarrow S_{SAM}=\dfrac{1}{2}S_{SAB}=\dfrac{a^2\sqrt{3}}{2}\)
\(\Rightarrow V_{SAMN}=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}.\dfrac{a^2\sqrt{3}}{2}=\dfrac{a^3}{4}\)
Lại có:
\(V_{SABC}=\dfrac{1}{3}SA.S_{ABC}=\dfrac{1}{3}.a\sqrt{3}.\dfrac{\left(2a\right)^2\sqrt{3}}{4}=a^3\)
\(\Rightarrow V_{A.BCMN}=V_{SABC}-V_{SANM}=\dfrac{3a^3}{4}\)




22.
\(sinx\le1\Rightarrow3sinx+2019\le3.1+2019=2022\)
Đáp án B
23.
\(C_n^3=\dfrac{A_n^3}{3!}=\dfrac{2022}{6}=337\)
Đáp án A

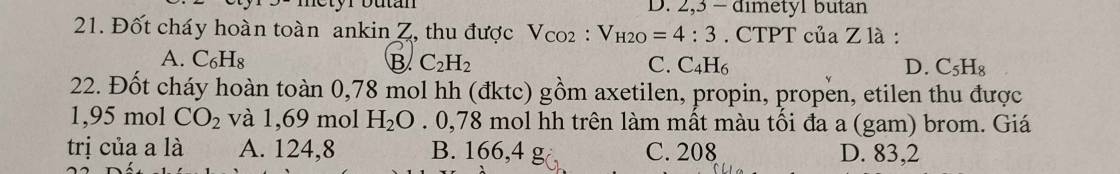




 câu 21 22 23 24 giúp mình nha
câu 21 22 23 24 giúp mình nha




Câu 21:
\(n_{C_2H_2}=\dfrac{4,032}{22,4}=0,18\left(mol\right)\)
BTNT C, có: \(n_{Ag_2C_2}=n_{C_2H_2}=0,18\left(mol\right)\)
\(\Rightarrow m_{Ag_2C_2}=0,18.240=43,2\left(g\right)\)
→ Đáp án: A
Câu 22:
nA = 0,25 (mol)
nCO2 = 1,25 (mol)
Gọi CTPT của A là CnH2n-2
\(\Rightarrow n=\dfrac{n_{CO_2}}{n_A}=5\)
Vậy: A là C5H8.
Đáp án: A