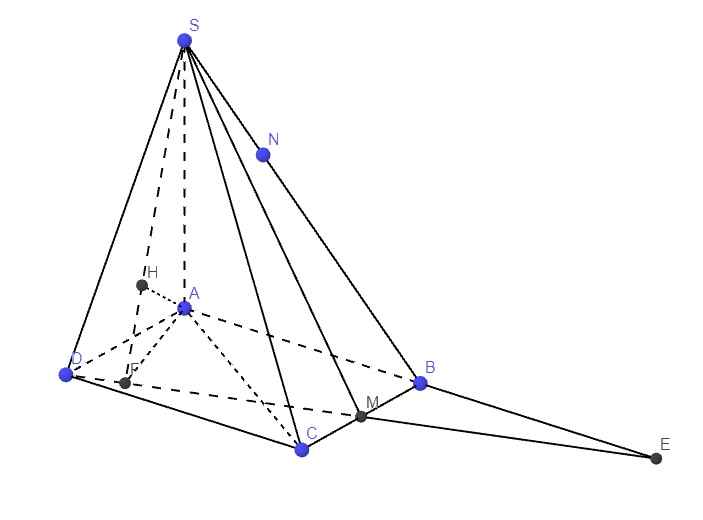
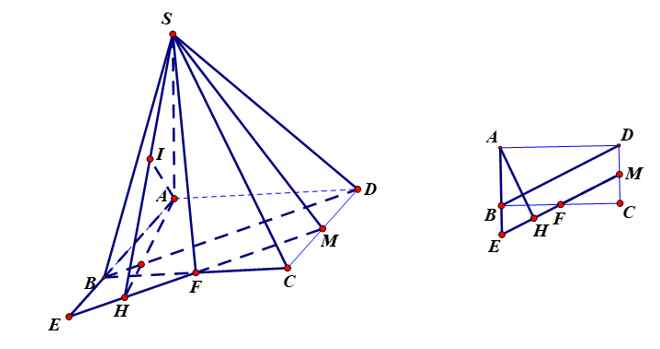
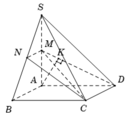
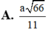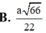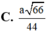Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a, AD=a√3, SD=a√7 và SA⊥(ABCD). Gọi M,N là trung điểm của SA và SB. Tính khoảng cách từ S đến mp (MND).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nối DM và AB kéo dài cắt nhau tại E
Do BM song song và bằng 1 nửa AD \(\Rightarrow BM\) là đường trung bình tam giác ADE
\(\Rightarrow AE=2BE\Rightarrow d\left(B;\left(SMD\right)\right)=\dfrac{1}{2}d\left(A;\left(SMD\right)\right)\)
Lại có: \(\left\{{}\begin{matrix}BN\cap\left(SMD\right)=S\\NS=\dfrac{1}{3}BS\end{matrix}\right.\) \(\Rightarrow d\left(N;\left(SMD\right)\right)=\dfrac{1}{3}d\left(B;\left(SMD\right)\right)=\dfrac{1}{6}d\left(A;\left(SMD\right)\right)\)
Từ A kẻ AF vuông góc MD (F thuộc MD), từ A kẻ AH vuông góc SF (H thuộc SF)
\(\Rightarrow AH\perp\left(SMD\right)\Rightarrow AH=d\left(A:\left(SMD\right)\right)\)
Hệ thức lượng trong tam giác vuông ADE:
\(\Rightarrow AF=\dfrac{AD.AE}{DE}=\dfrac{AD.2AB}{\sqrt{AD^2+\left(2AB\right)^2}}=\dfrac{8a\sqrt{17}}{17}\)
\(SA=\sqrt{SD^2-AD^2}=a\sqrt{21}\)
Hệ thức lượng: \(AH=\dfrac{SA.AF}{\sqrt{SA^2+AF^2}}=...\)
\(\Rightarrow d\left(N;\left(SMD\right)\right)=\dfrac{1}{6}AF=...\)

bẹn tk thay chữ vô thoy là đc:
Gọi  là trung điểm của
là trung điểm của  . Gọi
. Gọi  là giao điểm của
là giao điểm của  và
và 

 nên
nên  .
. .
.
Ta kẻ  , mặt khác
, mặt khác  .
.
Ta kẻ  .
. 
 .
.
Ta có 
 .
.
Ta có  là hình chữ nhật,
là hình chữ nhật,  .
.

Ta có  .
.
 ,
,

 .
.
Vậy  .
.

Đáp án B

Gọi K = C D ∩ A B khi đó BC là đường trung bình trong tam giác KAD nên KB =a
Gọi I = K N ∩ A M
Ta có
I M I A = M N K B = 1 2 ⇒ d M = 1 2 d A
Do C E = 1 2 A D nên Δ A C D vuông tại C
Dựng A H ⊥ N C ,
d A = A H = N A . A C N A 2 + A C 2 = a 66 11
Do đó d M = a 66 22

Chọn A.

Xác định được
![]()
Vì M là trung điểm SA nên
![]()
Kẻ AK ⊥ DM và chứng minh được AK ⊥ (CDM) nên
![]()
Trong tam giác vuông MAD tính được
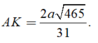

Xác định được ![]()
Vì M là trung điểm SA nên
![]()
Kẻ ![]() và chứng minh được
và chứng minh được ![]() nên
nên ![]()
Trong
∆
vuông MAD tính được ![]()
Chọn A.