Cho ∆ABC, vẽ tia Ax nằm giữa hai tia AB, AC. Gọi E và F là hình chiếu của B, C trên Ax. Chứng minh BE + CF ≥ BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 10 2019
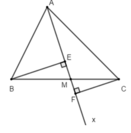
Vì BE ⊥ Ax tại E nên tam giác BEM vuông tại E ⇒ BM > BE (quan hệ đường xiên và đường vuông góc)
Vì CF ⊥ Ax tại F nên tam giác CFM vuông tại F ⇒ CM > CF (quan hệ đường xiên và đường vuông góc)
Khi đó ta có: BM + CM > BE + CF
Mà BM + CM = BC (M thuộc BC)
Do đó: BC > BE + CF hay BE + CF < BC.
Chọn đáp án A
8 tháng 7 2019
Bạn kiểm tra lại đề nhé! Tia Ax nằm giữa hai tia AD và AC hay hai tia AB và AC
Tham khảo đề bài và lời giải tại link:
Câu hỏi của Chử Văn Dũng - Toán lớp 7 - Học toán với OnlineMath
21 tháng 3 2016
a)xét tgAEB và tgADC có
A là góc chung
AE=AC(gt)
AB=AD(gt)
suy ra tgAEB = tgADC (c.g.c)
suy ra BE=AC(hai cạnh tương ứng
cho k trước đi rồi làm câu b;c;d cho
Tớ nghĩ đề đúng phải là \(BE+CF\le BC\)
Bạn xem lại đề nhé