cho tam giác ABC can tại A có CAB=40 độ.ĐƯờng trung trực của AB cắt BC tại D.Tính góc DAC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 12 2019
a) Xét \(\Delta\)DMB và \(\Delta\)DMC có:
DM chung
^DMB = ^DMC ( = 1v )
BM = MC ( M là trung điểm BC )
=> \(\Delta\)DMB = \(\Delta\)DMC ( c. g. c)
b) Từ (a) => ^DCM = ^DBM => ^ACB = ^EBC ( 1)
=> ^EAD = ^ACB = ^EBC = ^AED ( so le trong; AE// BC )
=> \(\Delta\)ADE cân tại D
=> DA = DE mà từ (a) => DB = DC
=> BE = AC ( 2)
Từ (1); (2) và cạnh BC chung
=> \(\Delta\)BEC = \(\Delta\)CAB.( c. g.c)
5 tháng 1 2022
Bài 3:
a: Xét ΔABD và ΔACD có
AB=AC
AD chung
BD=CD
Do đó: ΔABD=ΔACD
b: Ta có: ΔABD=ΔACD
nên \(\widehat{BAD}=\widehat{CAD}\)
c: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là đường cao
26 tháng 8 2021
a: Xét ΔACE vuông tại C và ΔADE vuông tại D có
AE chung
AC=AD
Do đó: ΔACE=ΔADE
Suy ra: \(\widehat{CAE}=\widehat{DAE}\)
hay AE là tia phân giác của \(\widehat{CAB}\)
b: Ta có: ΔACE=ΔADE
nên EC=ED
Ta có: AC=AD
nên A nằm trên đường trung trực của CD(1)
Ta có: EC=ED
nên E nằm trên đường trung trực của CD(2)
Từ (1) và (2) suy ra AE là đường trung trực của CD
KV
7 tháng 1
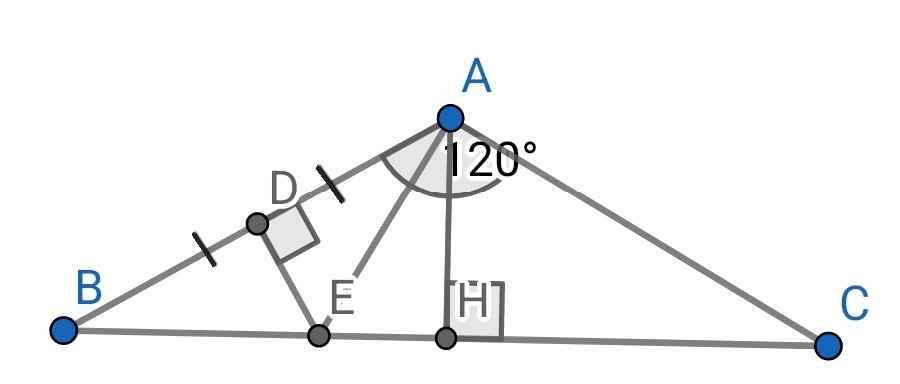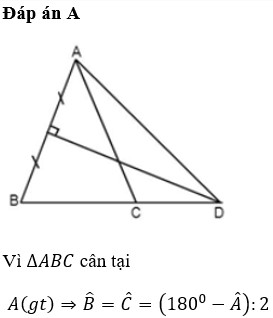
Do ∆ABC cân tại A (gt)
⇒ ∠B = ∠C = (180⁰ - ∠BAC) : 2
= (180⁰ - 120⁰) : 2
= 30⁰
∆AHB vuông tại H (do AH ⊥ BC)
⇒ ∠B + ∠BAH = 90⁰
⇒ ∠BAH = 90⁰ - ∠B
= 90⁰ - 30⁰
= 60⁰
Xét hai tam giác vuông: ∆AED và ∆BED có:
ED là cạnh chung
AD = BD (do D là trung điểm của AB)
⇒ ∆AED = ∆BED (hai cạnh góc vuông)
⇒ ∠EAD = ∠EBD = 30⁰ (hai góc tương ứng)
⇒ ∠EAH = ∠BAH - ∠EAD
= 60⁰ - 30⁰
= 30⁰
⇒ ∠EAH = ∠EAD
Xét hai tam giác vuông: ∆AEH và ∆AED có:
AE là cạnh chung
∠EAH = ∠EAD = 30⁰
⇒ ∆AEH = ∆AED (cạnh huyền - góc nhọn)
Mà ∆AED = ∆BED (cmt)
⇒ ∆BED = ∆AEH
HT
2
11 tháng 12 2021
\(\widehat{ACB}=180^0-\widehat{A}-\widehat{B}=60^0\left(\Delta ABC\right)\\ \Rightarrow\widehat{ACD}=\widehat{BCD}=\dfrac{1}{2}\widehat{ACB}=30^0\left(CD\text{ là phân giác }\widehat{ACB}\right)\\ \Rightarrow\left\{{}\begin{matrix}\widehat{CDA}=180^0-\widehat{A}-\widehat{ACD}=70^0\left(\Delta ACD\right)\\\widehat{CDB}=180^0-\widehat{CDA}=110^0\left(\text{kề bù}\right)\end{matrix}\right.\)
ND
Nguyễn Đức Trí
VIP
28 tháng 8 2023
a) Gọi H là giao điểm đường trung trực của EF và EF
Xét Δ KEF có :
KH là đường trung trực của EF
⇒ KH vừa là đường cao, trung tuyến của Δ KEF
⇒ Δ KEF là tam giác cân tại K
b) Xét Δ vuông DEF có :
\(\widehat{DEF}+\widehat{DFE}=90^o\)
\(\Rightarrow\widehat{DEF}=90^o-\widehat{DFE}\)
\(\Rightarrow\widehat{DEF}=90^o-40^o\)
\(\Rightarrow\widehat{DEF}=50^o\)
mà \(\widehat{DEK}+\widehat{KEF}=\widehat{DEF}\)
\(\widehat{KEF}=\widehat{DFE}=40^o\) (Δ KEF là tam giác cân tại K)
\(\Rightarrow\widehat{DEK}=\widehat{DEF}-\widehat{KEF}=50^o-40^o=10^o\)
góc ABC=góc ACB=(180-40)/2=70 độ
=>góc DAB=70 độ>góc CAB
=>AC nằm giữa AB và AD
=>góc DAC=70-40=30 độ