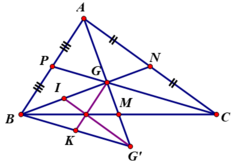
Gọi G là Trọng tâm của tam giác abc. Trên tia đối AG lấy G' sao cho G là trung điểm của AG . A) CM BG'=GC. B) Đường trung trực của cạnh BC lần lượt cắt AC , GC và BG' tại I , J và K . CM : BK = CJ . C) CM góc ICJ = IBJ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi I, K lần lượt là trung điểm của BG, BG’.
* M là trung điểm GG’⇒ BM là đường trung tuyến ΔBGG.
Mà M là trung điểm BC ⇒ BM = ½ .BC (4)
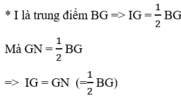
Xét ΔIGG’ và ΔNGA có:
IG = GN (chứng minh trên)
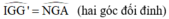
GG’ = GA (Vì G là trung điểm AG’)
⇒ ΔIGG’ = ΔNGA (c.g.c)
⇒ G’I = AN (hai cạnh tương ứng)
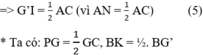
Mà GC = BG’ (chứng minh phần a))
⇒ Nên PG = BK.
ΔGMC = ΔG’MB (chứng minh câu a)

Xét ΔPGB và ΔKBG có:
PG = BK (chứng minh trên)
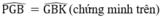
BG chung
⇒ ΔPGB = ΔKBG (c.g.c)
⇒ PB = GK (hai cạnh tương ứng)
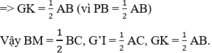

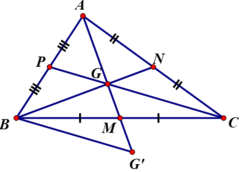
Gọi trung điểm BC, CA, AB lần lượt là M, N, P.
⇒ AM, BN, CP là các đường trung tuyến, G là trọng tâm của ΔABC
Theo tính chất đường trung tuyến của tam giác ta có:
GB = 2/3.BN (1)
GA = 2/3.AM, mà GA = GG’ (do G là trung điểm của AG’) ⇒ GG’ = 2/3.AM (2)
GM=1/2.AG, mà AG=GG’ ⇒ GM=1/2.GG’ ⇒ M là trung điểm của GG’ hay GM = G'M .
Xét ΔGMC và ΔG’MB có:
GM = G’M (chứng minh trên)
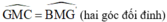
MC = MB
⇒ ΔGMC = ΔG’MB (c.g.c)
⇒ GC = G’B (hai cạnh tương ứng).
Mà CG = 2/3.CP (tính chất đường trung tuyến) ⇒ G’B = 2/3.CP (3)
Từ (1), (2), (3) ta có : GG’ = 2/3.AM , GB = 2/3.BN, G’B = 2/3.CP.

a: Gọi G là trọng tâm, M là trung điểm của BC
=>AG=2/3AM
BM+BE=EM
CM+CF=MF
mà BM=CM; BE=CF
nên EM=MF
=>M là trung điểm củaEF
Xet ΔAEF có
AM là trung tuyến
AG=2/3AM
=>G là trọng tâm của ΔAEF
b: G là trọng tâm cùa ΔAEF
=>N là trung điểm của AF
Xét ΔAEF có FM/FE=FN/FA
nên MN//AE và MN=1/2AE
Xét ΔGAE có GH/GA=GI/GE
nên HI//AE và HI=1/2AE
=>MN//HI và MN=HI
Gọi G là trọng tâm tam giác ABC. Trên tia AG lấy G' sao cho G là trung điểm AG':
a)Chứng minh BG'=CG
b)Đường trung trực của cạnh BC cắt CA,CG và BG' lần lượt tại I,J,K. Chứng minh BK=CJ
c)Chứng minh góc ICJ= góc IBJ