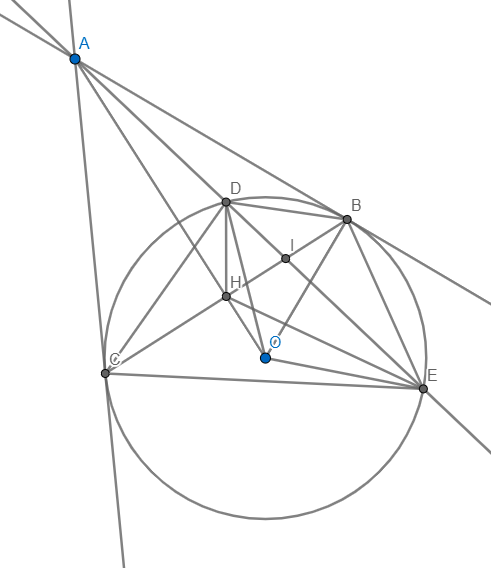
qua điểm A nằm ngoài đường tròn (O) vẽ 2 tiếp tuyến AB và AC và cẽ cát tuyến ADE của (O) sao cho tâm O nằm trong góc EAC.
a) Chứng minh OA vuông góc BC tại H và AB .AC = AD.AE
b) Chứng minh tứ giác OHDE nooijt iếp
c) Gọi K là giao điểm của DE và BC . Chứng minh AD.KE= AE.KD
d) Gọi M là điểm đối xứng ủa B qua E . AM cắt BC tại N. CHứng minh ND // BM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc OBA+góc OCA=180 độ
=>OBAC nội tiếp
Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
=>OA là trung trực của BC
=>OA vuông góc BC tại I
b: ΔOBA vuông tại B có BI vuông góc OA
nên OI*IA=BI^2=BC^2/4
Xét ΔABD và ΔAEB có
góc ABD=góc AEB
góc BAD chug
=>ΔABD đồng dạng với ΔAEB
=>AB/AE=AD/AB
=>AB^2=AD*AE=AH*AO

a: Xet ΔABD và ΔAEB có
góc ABD=góc AEB
góc BAD chung
=>ΔABD đồng dạngvới ΔAEB
=>AB/AE=AD/AB
=>AB^2=AD*AE
b: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC
=>AH*AO=AB^2=AD*AE
=>AH/AE=AD/AO
=>ΔAHD đồng dạng với ΔAEO
=>góc AHD=góc AEO
=>góc OHD+góc OED=180 độ
=>OHDE nội tiếp

a) Vì AB,AC là tiếp tuyến \(\Rightarrow\Delta ABC\) cân tại A có AO là phân giác \(\angle BAC\)
\(\Rightarrow OA\bot BC\)
Xét \(\Delta ABD\) và \(\Delta AEB:\) Ta có: \(\left\{{}\begin{matrix}\angle ABD=\angle AEB\\\angle EABchung\end{matrix}\right.\)
\(\Rightarrow\Delta ABD\sim\Delta AEB\left(g-g\right)\Rightarrow\dfrac{AB}{AE}=\dfrac{AD}{AB}\Rightarrow AB^2=AD.AE\)
b) tam giác ABO vuông tại B có đường cao BH nên áp dụng hệ thức lượng
\(\Rightarrow AB^2=AH.AO\Rightarrow AH.AO=AD.AE\Rightarrow\dfrac{AH}{AE}=\dfrac{AD}{AO}\)
Xét \(\Delta AHD\) và \(\Delta AEO:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{AH}{AE}=\dfrac{AD}{AO}\\\angle EAOchung\end{matrix}\right.\)
\(\Rightarrow\Delta AHD\sim\Delta AEO\left(c-g-c\right)\Rightarrow\angle AHD=\angle AEO\Rightarrow DEOH\) nội tiếp
c) Ta có: \(\angle BHE=90-\angle OHE=90-\angle ODE\) (DEOH nội tiếp)
\(=90-\dfrac{180-\angle DOE}{2}=\dfrac{1}{2}\angle DOE=\dfrac{1}{2}\angle DHE\) (DEOH nội tiếp)
\(\Rightarrow HB\) là phân giác \(\angle DHE\Rightarrow\dfrac{ID}{IE}=\dfrac{DH}{HE}\)
Vì HB là phân giác \(\angle DHE\) và \(HA\bot HB\Rightarrow HA\) là phân giác ngoài \(\angle DHE\)
\(\Rightarrow\dfrac{AD}{AE}=\dfrac{DH}{HE}=\dfrac{ID}{IE}\Rightarrow AD.IE=ID.AE\)
a) Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: AB=AC(Tính chất hai tiếp tuyến cắt nhau)
Ta có: AB=AC(cmt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: OB=OC(=R)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay OA\(\perp\)BC tại H
Xét ΔADB và ΔABE có
\(\widehat{BAD}\) chung
\(\widehat{ABD}=\widehat{AEB}\left(=\dfrac{1}{2}sđ\stackrel\frown{BD}\right)\)
Do đó: ΔADB\(\sim\)ΔABE(g-g)
Suy ra: \(\dfrac{AD}{AB}=\dfrac{AB}{AE}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=AD\cdot AE\)

a) Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: AB=AC(Tính chất hai tiếp tuyến cắt nhau)
Ta có: AB=AC(cmt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: OB=OC(=R)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
hay OA⊥BC(đpcm)

a: Xét (O) có
AB,AC là tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC tại H
=>AH*AO=AB^2
Xet ΔABD và ΔAEB có
góc ABD=góc AEB
góc BAD chung
=>ΔABD đồng dạng với ΔAEB
=>AB/AE=AD/AB
=>AB^2=AE*AD=AH*AO
b: AE*AD=AH*AO
=>AE/AH=AO/AD
=>ΔAEO đồng dạng với ΔAHD
=>góc AHD=góc AEO
=>góc OHD+góc OED=180 độ
=>OEDH là tứ giác nội tiếp

a: Xét tứ giác OIBA có \(\widehat{OIA}=\widehat{OBA}=90^0\)
nên OIBA là tứ giác nội tiếp
b: Xét ΔACD và ΔAEC có
\(\widehat{ACD}=\widehat{AEC}\)
\(\widehat{DAC}\) chung
Do đó: ΔACD\(\sim\)ΔAEC
SUy ra: AC/AE=AD/AC
hay \(AC^2=AE\cdot AD\left(1\right)\)
c: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
mà OB=OC
nên OA là đường trung trực của BC
Xét ΔOCA vuông tại C có CK là đường cao
nên \(AK\cdot AO=AC^2\left(2\right)\)
Từ (1) và (2) suy ra \(AK\cdot AO=AD\cdot AE\)
hay AK/AE=AD/AO
Xét ΔAKD và ΔAEO có
AK/AE=AD/AO
góc KAD chung
DO đó: ΔAKD\(\sim\)ΔAEO
Suy ra: \(\widehat{AKD}=\widehat{AEO}\)


a) Hai tam giác vuông ABO và ACO có chung cạnh huyền AO nên A, B, O, C cùng thuộc đường tròn đường kính AO.
Vậy tứ giác ABOC là tứ giác nội tiếp.
b) Ta thấy ngay \(\Delta ABD\sim\Delta AEB\left(g-g\right)\)
\(\Rightarrow\frac{AB}{AE}=\frac{AD}{AB}\Rightarrow AE.AD=AB^2\)
Xét tam giác vuông ABO có BH là đường cao nên áp dụng hệ thức lượng ta có:
\(AH.AO=AB^2\)
Suy ra AD.AE = AH.AO
c) Ta có \(\widehat{PIK}+\widehat{IKQ}+\widehat{P}+\widehat{Q}=360^o\)
\(\Rightarrow2\left(\widehat{PIO}+\widehat{P}+\widehat{OKQ}\right)=360^o\)
\(\Rightarrow\widehat{PIO}+\widehat{P}+\widehat{OKQ}=180^o\)
Mặt khác \(\widehat{PIO}+\widehat{P}+\widehat{IOP}=180^o\)
\(\Rightarrow\widehat{IOP}=\widehat{OKQ}\Rightarrow\Delta PIO\sim\Delta QOK\)
\(\Rightarrow\frac{IP}{PO}=\frac{OQ}{KQ}\Rightarrow PI.KQ=PO^2\)
Sử dụng bất đẳng thức Cô-si ta có:
\(IP+KQ\ge2\sqrt{IP.KQ}=2\sqrt{OP^2}=PQ\)
acje cho hỏi 2 tam giác đồng dạng ở câu b là góc nào í chỉ ro rõ cho e với ạk

c) Cần chứng minh AD/AE= DK/KE
HK là phân giác góc DHE => DK/KE=DH/HE (1)
Tam giác ADH~AOE => DH/AD=OE/AO
Tam giác ADO~AHE => OD/AO=HE/AE
Vì OE/AO=OD/AO= > DH/AD=HE/AE => DH/HE= AD/AE(2)
Từ 1-2 => AD/AE= DK/KE => đpcm
d) Kẻ DN'//BE với N' thuộc BC. Kéo dài AN' cắt BE tại M'. Chứng minh BE=EM' là xong.
Sử dụng talet và tam giác đồng dạng suy ra tỷ số DN'/BE=DN'/EM' => BE=EM' nhé.