Cho ∆ABC có AB=AC.Kẻ tia phân giác AD của góc BAC (D thuộc BC)
a. Chứng minh ∆ABD=∆ACD
b. BD=CD
c. Chứng minh AD thuộc BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BV
Bùi Việt Hưng
14 tháng 3 2023
Đúng(0)
Những câu hỏi liên quan
14 tháng 11 2016
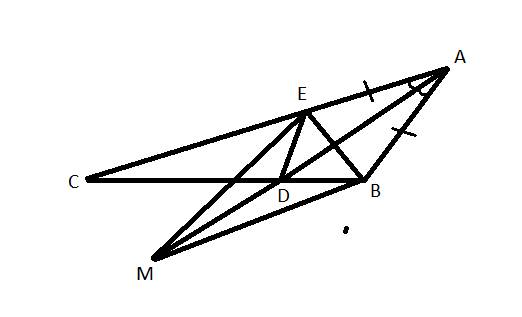
Bài 2:
Nối C với D ta được đoạn thẳng CD
Nối C với B, B với D, D với A, A với C, A với B ( Nói chung là gần giống vs hình của hoàng thị ngọc anh)
a)Xét tam giác ABC và tam giác ABD có:
AB chung
BC=AC (cùng cung tròn tâm A và B, bán kính AB)(gọi giải thích này là(1))
BD=AD (như trên)
-> 2 tam giác này bằng nhau(2)
b)Xét tam giác ACD và tam giác BCD có:
CD chung
AC=BC (1)
AD=BD (1)
-> 2 tam giác này bằng nhau
c) vì tam giác ABC bằng tam giác ABD (2)
-> góc CAB bằng góc BAD (2 góc tương ứng)
vậy AB là tpg của góc A
14 tháng 11 2016
a) Vì AC thuộc đường tròn (A;AB)
AD thuộc đg tròn (A;AB)
=> AC = AD
Tượng tự: BC thuộc đg tròn (B;AB)
BD thuộc đg tròn (B;AB)
=> BC = BD
Xét tg ABC và tg ABD có:
AC = AD ( c/m trên)
AB cạnh chung( GT)
BC = BD ( c/m trên)
=> ΔABC = ΔABD ( c.c.c)→ ĐPCM
Ttự: AC ϵ (A; AB)
BC ϵ (B; AB). Do 2 đg tròn có bán kính bằng nhau
=> AC = BC
TT: AD = BD
Xét ΔACD và ΔBCD có:
AC = BC (c/m trên)
CD cạnh chung
AD = BD ( c/m trên)
=> ΔACD = ΔBCD(c.c.c)→ ĐPCM
24 tháng 12 2021
a: Xét ΔABD và ΔACD có
AB=AC
AD chung
BD=CD
Do đó: ΔABD=ΔACD
12 tháng 5 2019
C1 :
Hình : tự vẽ
a )Vì CA=CB ( đề bài cho ) => tam giác ABC cân tại C
mà CI vuông góc vs AB => CI là đường cao của tam giác ABC
=> CI cũng là đường trung tuyến của tam giác ABC ( t/c tam giác cân )
=> IA=IB (đpcm)
12 tháng 5 2019
C1 :
b) Có IA=IB ( cm phần a )
mà IA+IB = AB
IA + IA = 12 (cm)
=> IA = \(\frac{12}{2}=6\left(cm\right)\)
Xét tam giác vuông CIA có : CI2 + IA2 = CA2 ( Đ/l Py-ta -go )
CI2 + 62 = 102
CI2 = 102 - 62 = 64
=> CI = \(\sqrt{64}=8\left(cm\right)\)
Vậy CI ( hay IC ) = 8cm
15 tháng 12 2016
a) Xét tam giác ABD và tam giác ACD, có:
AB = AC ( Giả thiết ) (1)
AD chung (2)
Góc BAD = CAD ( D là tia phân giác của góc A ) (3)
Từ (1); (2); (3) => tam giác ABC = tam giác ACD ( c-g-c)
b) Tam giác ABC = tam giác ACD => DB = DC ( 2 cạnh tương ứng ).
Chúc bạn học tốt!
25 tháng 4 2023
a: Xét ΔABD và ΔACD có
AB=AC
góc BAD=góc CAD
AD chung
=>ΔABD=ΔACD
c: ΔABC cân tại A
mà AD là phân giác
nen AD vuông góc BC
Xét ΔABC có
AD,BE,CK là các đường cao
=>AD,BE,CK đồng quy