một canô đi từ A đến B rồi quay về lại từ B đến A Vận tốc thức của canô là 20 km/h Tính khoảng cách giữa hai bến AB biết thời gian cả đi lẫn về là 8h20 và vận tốc của dòng nước là 4 km/h
Mình cần gấp ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
12 tháng 3 2023
Đúng(1)
Những câu hỏi liên quan
NH
11 tháng 3 2023
đổi 8 giờ 20 phút = `25/3` giờ
gọi độ dài quãng đường AB là: x (đơn vị:km, x>0)
vận tốc xuôi dòng của cano là: `20+4=24`(km/h)
=> thời gian mà cano khi đi xuôi dòng là: `x/24` (giờ)
vận tốc ngược dòng của cano là: `20-4=16`(km/h)
=> thời gian mà cano đi ngược dòng là: `x/16` (giờ)
vì tổng thời gian đi và về là 8 giờ 20 phút nên ta có phương trình sau
`x/24+x/16=25/3`
`<=>x(1/24+1/16)=25/3`
`<=>x*5/48=25/3`
`<=>x=80(tm)`
khoảng cách giữa A và B là: 80km
VD
16 tháng 6 2023
Gọi vận tốc dòng nước là x (km/h) (x>0)
=> vận tốc xuôi dòng là x+12;
vận tốc ngược dòng là x-12
Thời gian xuôi dòng là 30/12+x;
ngược dòng là 30/x-12
Theo đề bài: 30/12+x + 30/x-12 = 16/3
=> (360 - 30x + 360 + 30x) / (144-x^2) = 16/3
=> 720/(144-x^2) = 16/3
=> 144-x^2 = 720 : 16/3 = 135
=> x^2 = 144 - 135 = 9
=> x = 3 (x>0)
Vậy vận tốc dòng nước là 3 km/h
9 tháng 11 2018
vận tốc xuôi dòng là Vxuôi= V+ Vnước
Vận tốc ngược dong là Vngược =V - Vnước
Thoi gian ca nô đi từ bờ A đến B rồi quay ngược lại vế A là:
t=\(\frac{s}{V_{xuoi}}+\frac{s}{V_{nguoc}}=\frac{s}{V+V_{nc}}+\frac{s}{V-V_{nc}}\)
\(=\frac{s\left(V-V_{nc}\right)}{\left(V+V_{nc}\right)\left(V-V_{nc}\right)}+\frac{s\left(V+V_{nc}\right)}{\left(V-V_{nc}\right)\left(V+V_{nc}\right)}\)
\(=\frac{s\left(V-4\right)+s\left(V+4\right)}{\left(V+4\right)\left(V-4\right)}=\frac{s\left(V-4+V+4\right)}{V^2-16}=\frac{2s.V}{V-16}\)
12 tháng 5 2022
-Gọi khoảng cách giữa bến A và bến B là x (km) (x>0).
-Vận tốc của ca nô ngược dòng là: \(36-3-3=30\) (km/h).
-Thời gian đi xuôi là: \(\dfrac{x}{36}\left(h\right)\)
-Thời gian đi ngược là: \(\dfrac{x}{30}\left(h\right)\)
-Theo đề bài ta có phương trình sau:
\(\dfrac{x}{30}-\dfrac{x}{36}=\dfrac{2}{3}\)
\(\Leftrightarrow x\left(\dfrac{1}{30}-\dfrac{1}{36}\right)=\dfrac{2}{3}\)
\(\Leftrightarrow x.\dfrac{1}{180}=\dfrac{2}{3}\)
\(\Leftrightarrow x=120\left(nhận\right)\)
-Vậy khoảng cách giữa bến A và bến B là 120 km.
19 tháng 11 2017
https://h.vn/hoi-dap/tim-kiem?q=M%E1%BB%99t+chi%E1%BA%BFc+xu%E1%BB%93ng+m%C3%A1y+chuy%E1%BB%83n+%C4%91%E1%BB%99ng+tr%C3%AAn+1+d%C3%B2ng+s%C3%B4ng.N%E1%BA%BFu+thuy%E1%BB%81n+ch%E1%BA%A1y+xu%C3%B4i+d%C3%B2ng+t%E1%BB%AB+A---%3E+B+m%E1%BA%A5t+2+h.+N%E1%BA%BFu+ch%E1%BA%A1y+ng%C6%B0%E1%BB%A3c+d%C3%B2ng+th%C3%AC+m%E1%BA%A5t+4+h+.+T%C3%ADnh+v%E1%BA%ADn+t%E1%BB%91c+thuy%E1%BB%81n+khi+n%C6%B0%E1%BB%9Bc+l%E1%BA%B7ng+v%C3%A0+v%E1%BA%ADn+t%E1%BB%91c+n%E1%BB%A9%C6%A1c+so+v%E1%BB%9Bi+b%E1%BB%9D+bi%E1%BA%BFt+AB+=+60+kmGi%E1%BA%A3i+gi%C3%BAp+m%C3%ACnh+v%E1%BB%9Bi+%E1%BA%A1+!!!!!!!!!!+C%E1%BA%A3m+%C6%A1n+trc+nha+%3C30+c%C3%A2u+tr%E1%BA%A3+l%E1%BB%9DiV%E1%BA%ADt+l%C3%BD+l%E1%BB%9Bp+8+C%C6%A1+h%E1%BB%8Dc+l%E1%BB%9Bp+8Chuy%E1%BB%83n+%C4%91%E1%BB%99ng+c%C6%A1+h%E1%BB%8Dc&id=131334
Sao chép rồi dán link tìm kiếm
Y
20 tháng 6 2023
Gọi \(\left(1\right):\) ca nô
\(\left(2\right):\) nước
\(\left(3\right):\) bờ
\(v_{23}=6km/h\)
\(s=24km;t=1h\)
\(a,v_{12}=?\)
\(b,t'=?\)
=======================
\(a,\)Vận tốc của ca nô chuyển động từ A đến B là :
\(v_{13}=\dfrac{s}{t}=\dfrac{24}{1}=24km/h\)
Ta có : \(\overrightarrow{v_{13}}=\overrightarrow{v_{12}}+\overrightarrow{v_{23}}\)
Vì tàu xuôi dòng nên :
Tốc độ \(v_{13}=v_{12}+v_{23}\)
\(\Rightarrow24=v_{12}+6\)
\(\Rightarrow v_{12}=18\left(km/h\right)\)
\(b,\) Vì tốc độ đi ngược dòng nên \(v_{23}'=-6km/h\)
Thời gian để ca nô quay từ B về A là :
\(t'=\dfrac{s}{|v_{23}'|}=\dfrac{24}{\left|-6\right|}=4\left(h\right)\)
1 tháng 6 2017
Gọi vận tốc của cano là :x km/h
Vận tốc khi xuôi dòng của cano là : x+4 km/h
Vận tốc khi ngược dòng của cano là : x -4 km/h
thời gian cano đi xuôi dòng : 48 : (x+4) giờ
thời gian cano đi ngược dòng là : 48 :(x-4) giờ
có phương trình :
\(\frac{48}{x+4}+\frac{48}{x-4}=5\Leftrightarrow48\left(x+4\right)+48\left(x-4\right)=5\left(x^2-16\right)\)
\(\Leftrightarrow5x^2-96x-80=0\Leftrightarrow\orbr{\begin{cases}x=20\\x=-0,8\left(L\right)\end{cases}}\)
Vậy vận tốc cano Là : 20km/h
11 tháng 4 2018
- gọi vận tốc của canô lúc nước yên lặng là x (km/h)
- vận tốc cano xuôi dòng là x+4 (km/h)
- vận tốc cano ngược dòng là x - 4 (km/h)
- thời gian canô xuôi dòng là 48/x+4 (h)
- thời gian cano ngược dòng là 48/x-4 (h)
theo đề bài ta có phương trình
48/x+4 + 48/x-4 = 5
<=> 48(x-4)/(x+4)(x-4) + 48(x+4)/(x+4)(x-4) = 5(x+4)(x-4)/(x+4)(x-4)
=> 48x - 192 + 48x + 192 = 5x2 - 80
<=> 48x - 192 + 48x + 192 - 5x2 + 80 =0
<=> -5x2 + 96x + 80 = 0
x1 = 20 ( nhận)
x2 = -4/5 (loại)
vậy vân tốc cano khi nước yên lặng là 20 km/h
CM
6 tháng 10 2019
Gọi vận tốc thực của canô là x (km/h) (x > 3)
Gọi vận tốc xuôi dòng là : x + 3 (km/h)
Gọi vận tốc khi ngược dòng là : x – 3 (km/h)
Do kể từ lúc khởi hành đến khi về tới bến A hết tất cả 6 h nên ta có:
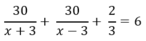
⇔ 30.3 (x- 3) + 30.3. (x+ 3) + 2(x+ 3). (x – 3) = 6.3.(x+3).(x – 3)
⇔ 90.(x – 3) + 90(x+ 3)+ 2(x2 – 9) = 18 (x2 -9)
⇔ 90x – 270+ 90x + 270 + 2x2 – 18 = 18x2 – 162
⇔ 180x + 2x2 – 18 = 18x2 – 162
⇔ 16x2 – 180x -144= 0
⇔ 4x2 –45x – 36 = 0
Có a=4; b= - 45, c= - 36
∆= ( -45)2 – 4.4.(- 36)= 2601 > 0
Phương trình đã cho có hai nghiệm là:
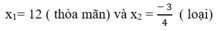
Vậy vận tốc của canô trong nước yên lặng là 12km/h.