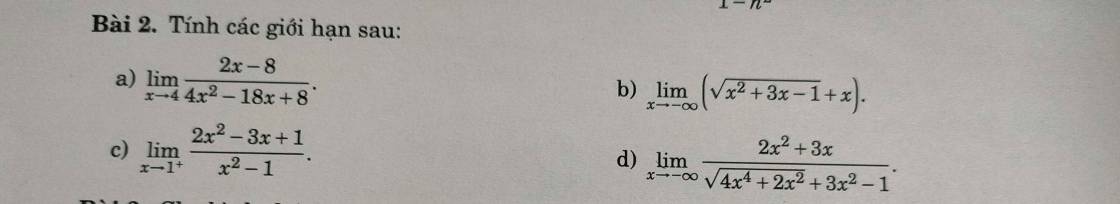 Giúp mình bài 2
Giúp mình bài 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


tiêu đề bài hai có nghĩa là j zậy bnnnnnnnnnnnnnnnn
mk nhát đọc đề quá

Bài 1:
a: Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó: ΔABI=ΔACI

2.
\(cosx+cos3x=1+\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow2cos2x.cosx=1+cos2x+sin2x\)
\(\Leftrightarrow2cos2x.cosx=2cos^2x+2sinx.cosx\)
\(\Leftrightarrow cosx\left(cos2x-cosx-sinx\right)=0\)
\(\Leftrightarrow cosx\left(cos^2x-sin^2x-cosx-sinx\right)=0\)
\(\Leftrightarrow cosx\left(cosx+sinx\right)\left(cosx-sinx-1\right)=0\)
\(\Leftrightarrow cosx.\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right).\left[\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)-1\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sin\left(x+\dfrac{\pi}{4}\right)=0\\cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\\x+\dfrac{\pi}{4}=\pm\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\\x=k2\pi\end{matrix}\right.\)
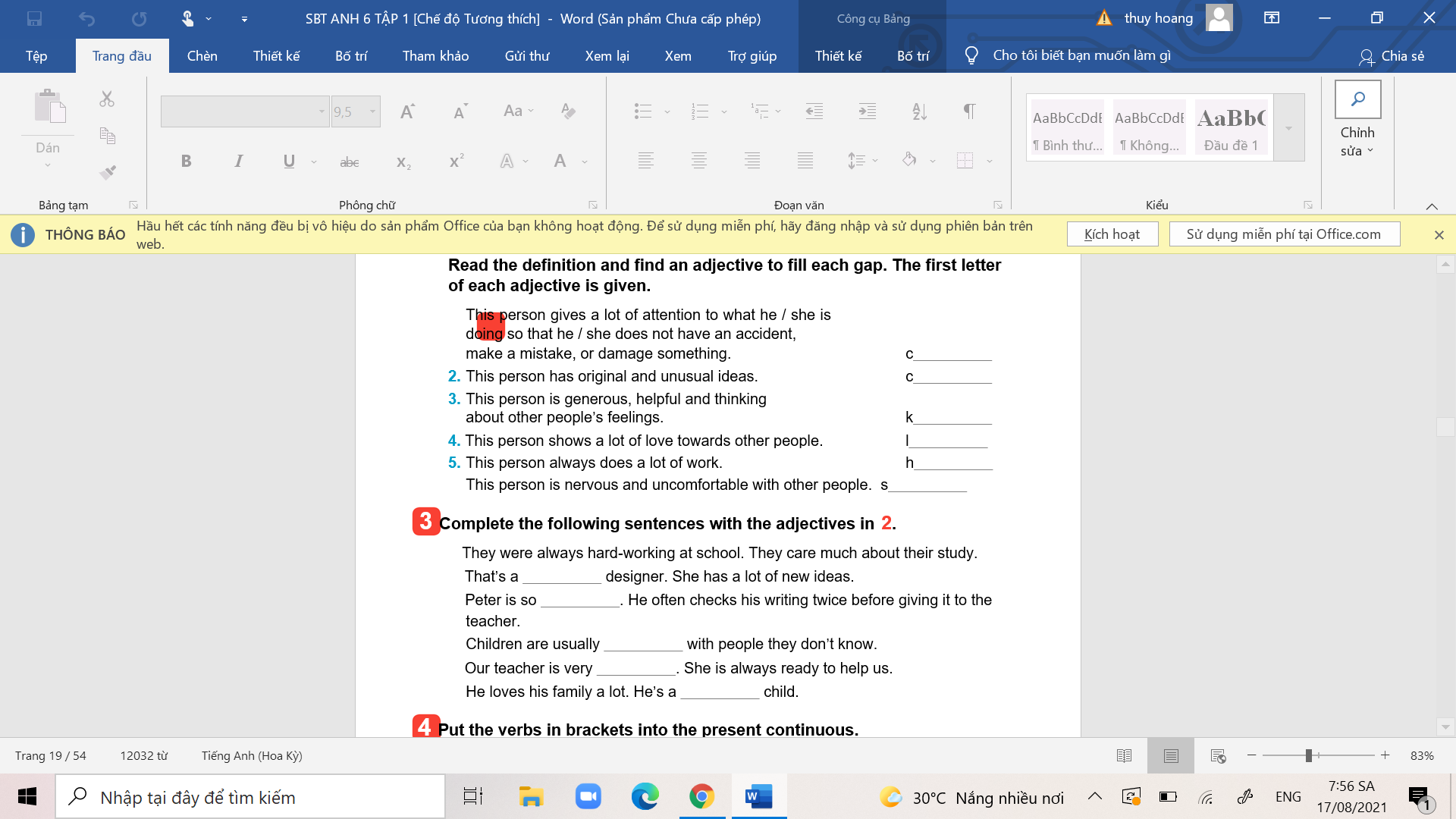 mn giúp mình bài 2, bài 3
mn giúp mình bài 2, bài 3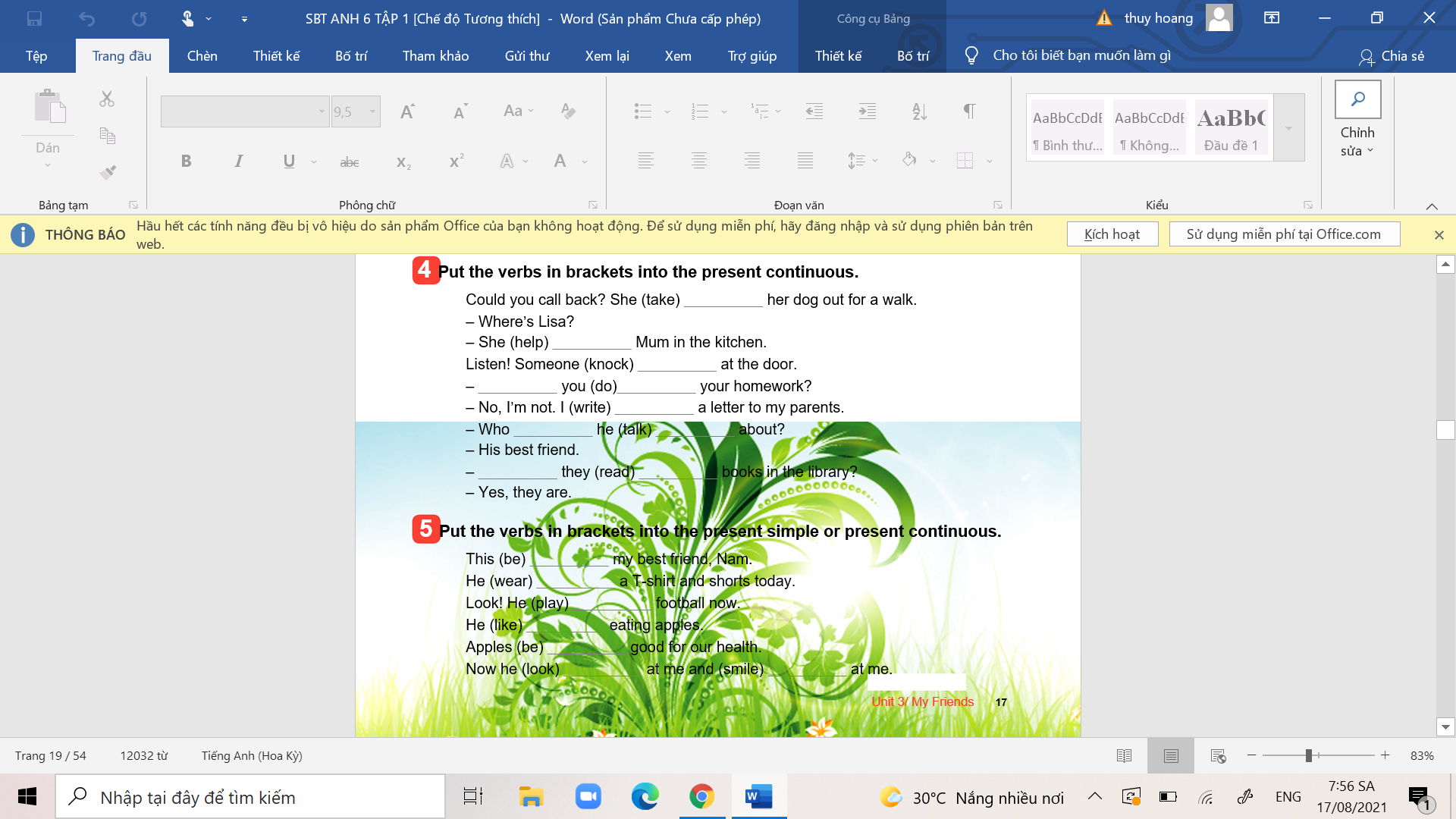 giúp mình bài 4 bài 5 ạ
giúp mình bài 4 bài 5 ạ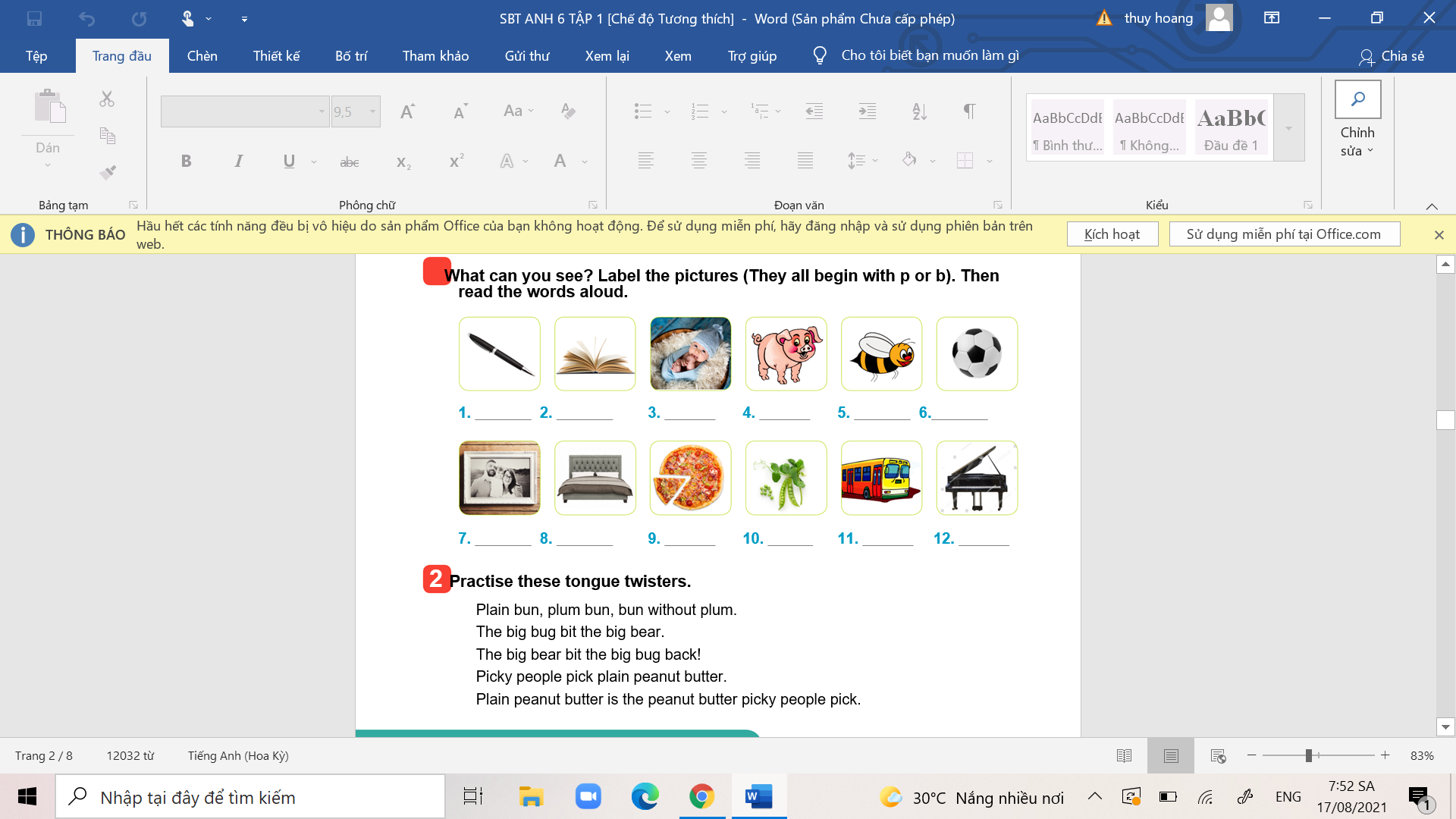 giúp mình bài 1.
giúp mình bài 1.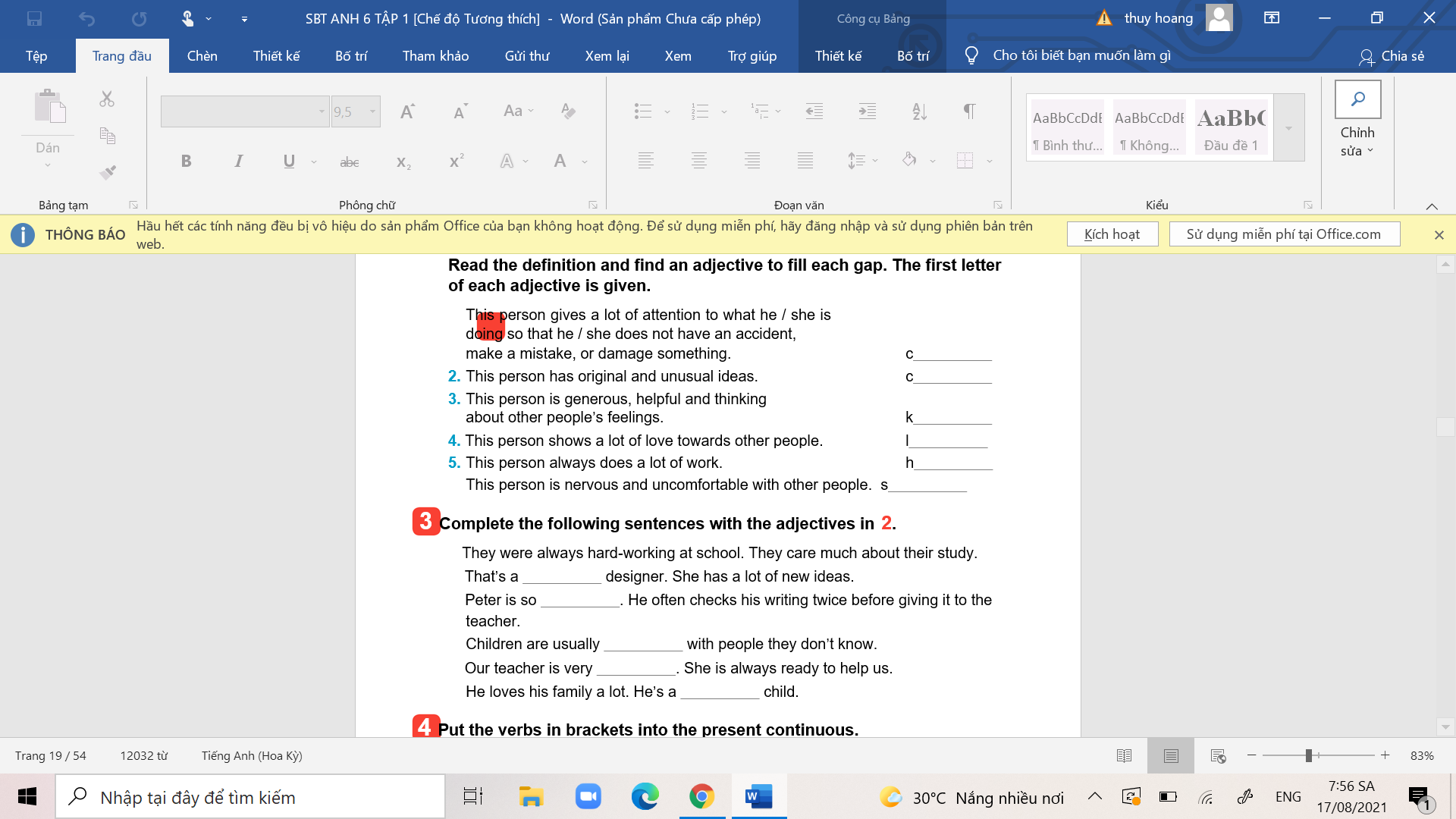 giúp mình bài 2. bài 3
giúp mình bài 2. bài 3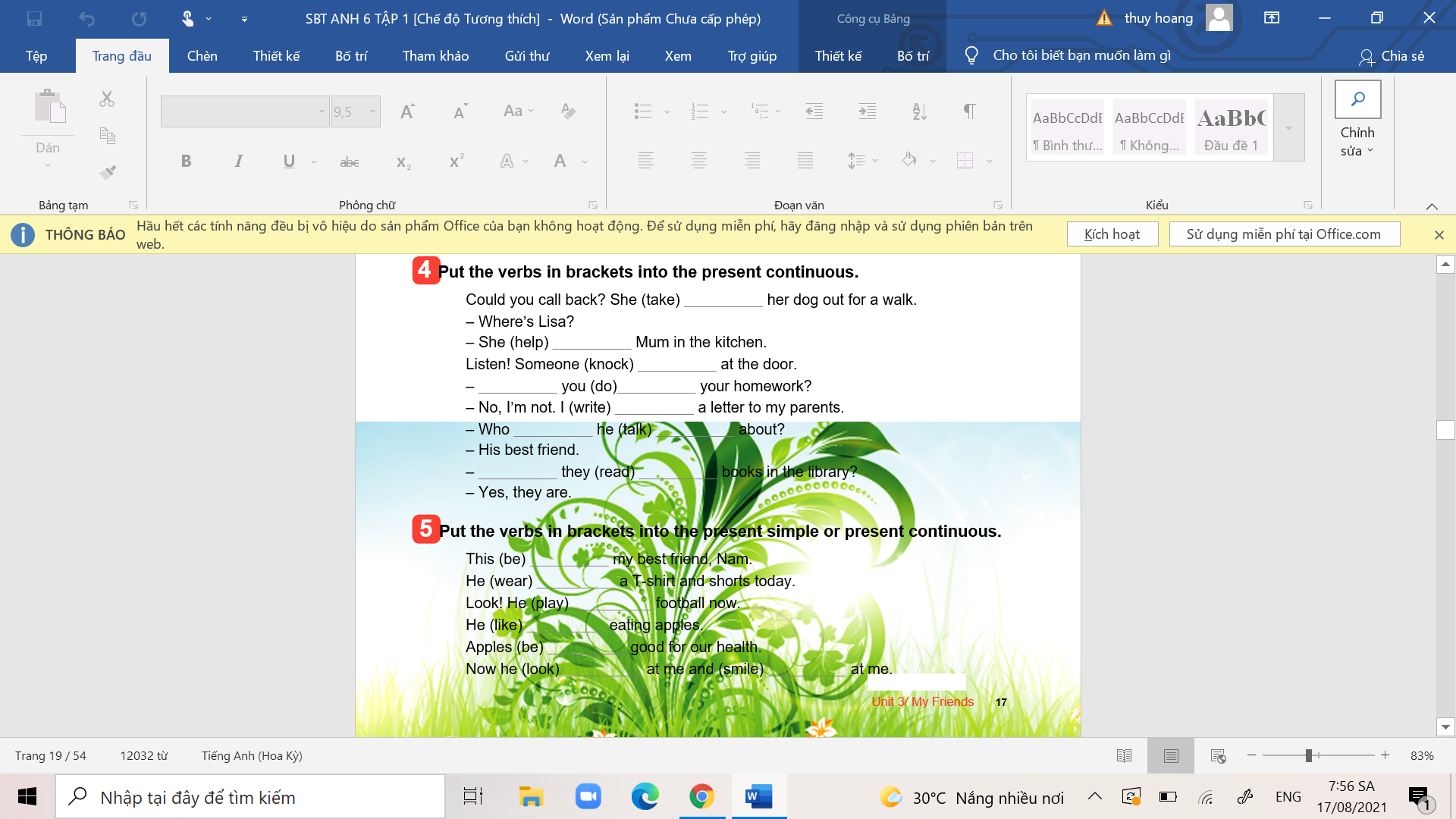 giúp mình bài 4, bài 5.
giúp mình bài 4, bài 5.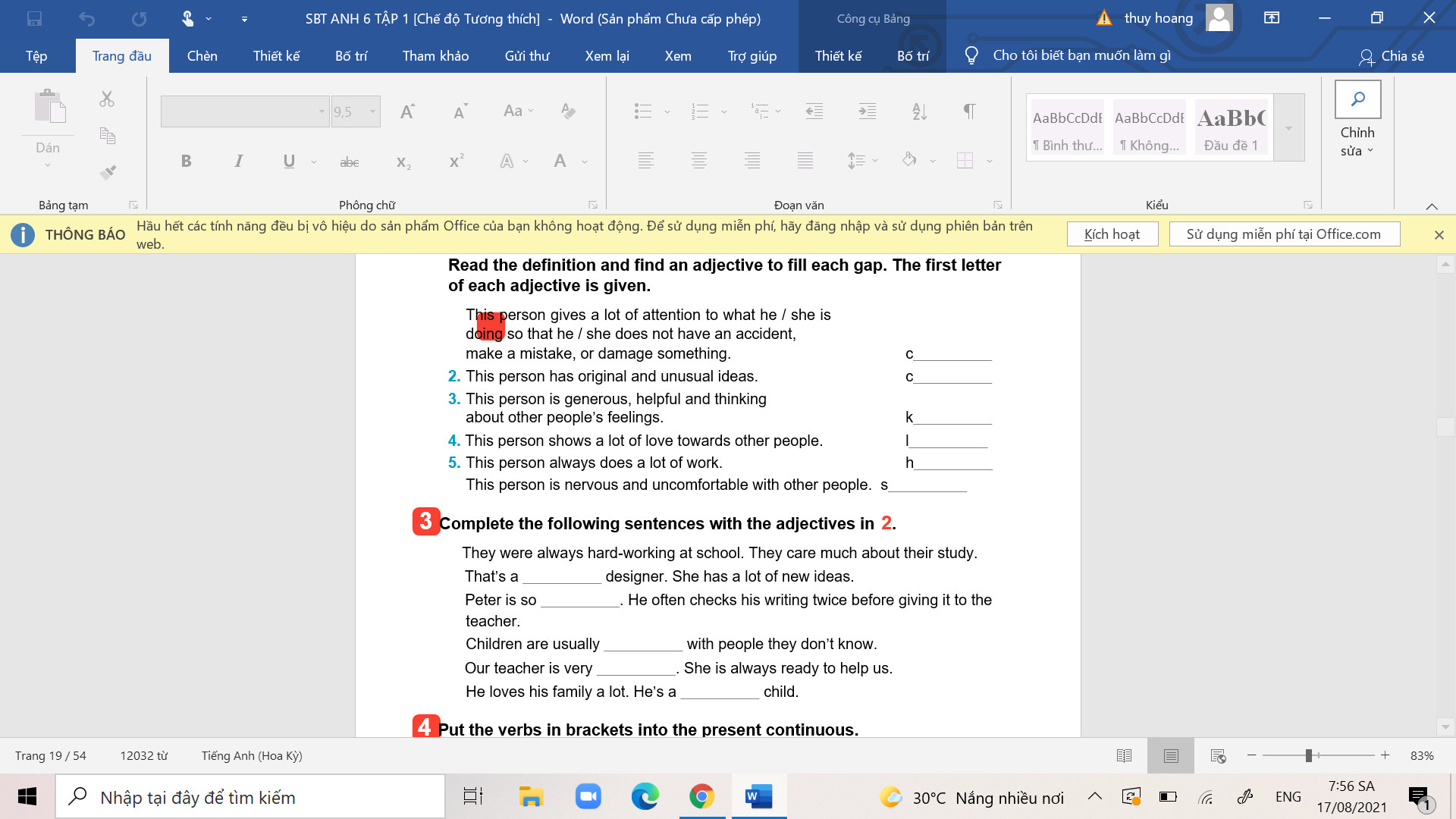 các bn giúp mình bài 2, bài 3.
các bn giúp mình bài 2, bài 3.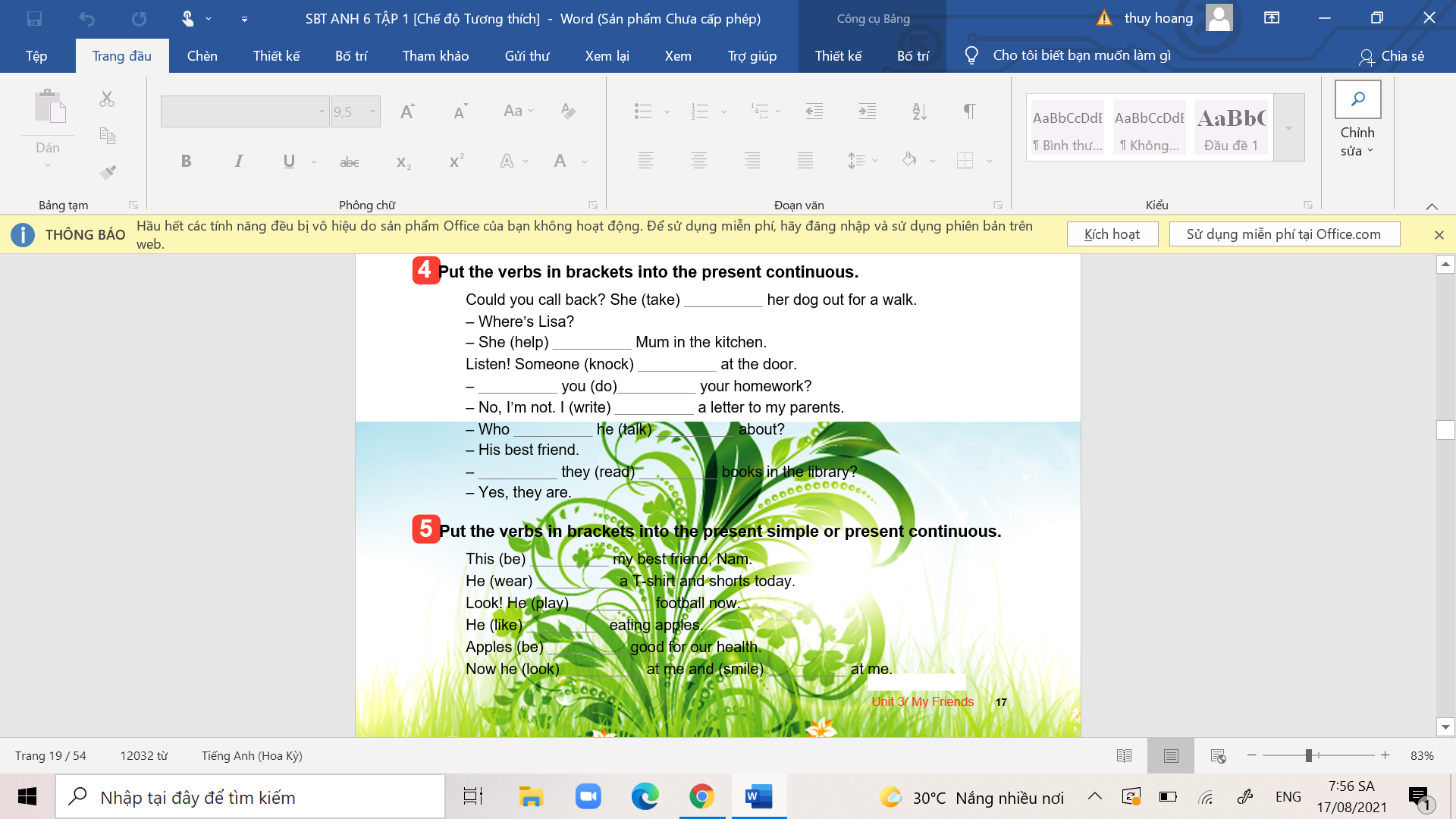 các bn giúp mình bài 4 và bài 5 nhé.
các bn giúp mình bài 4 và bài 5 nhé. 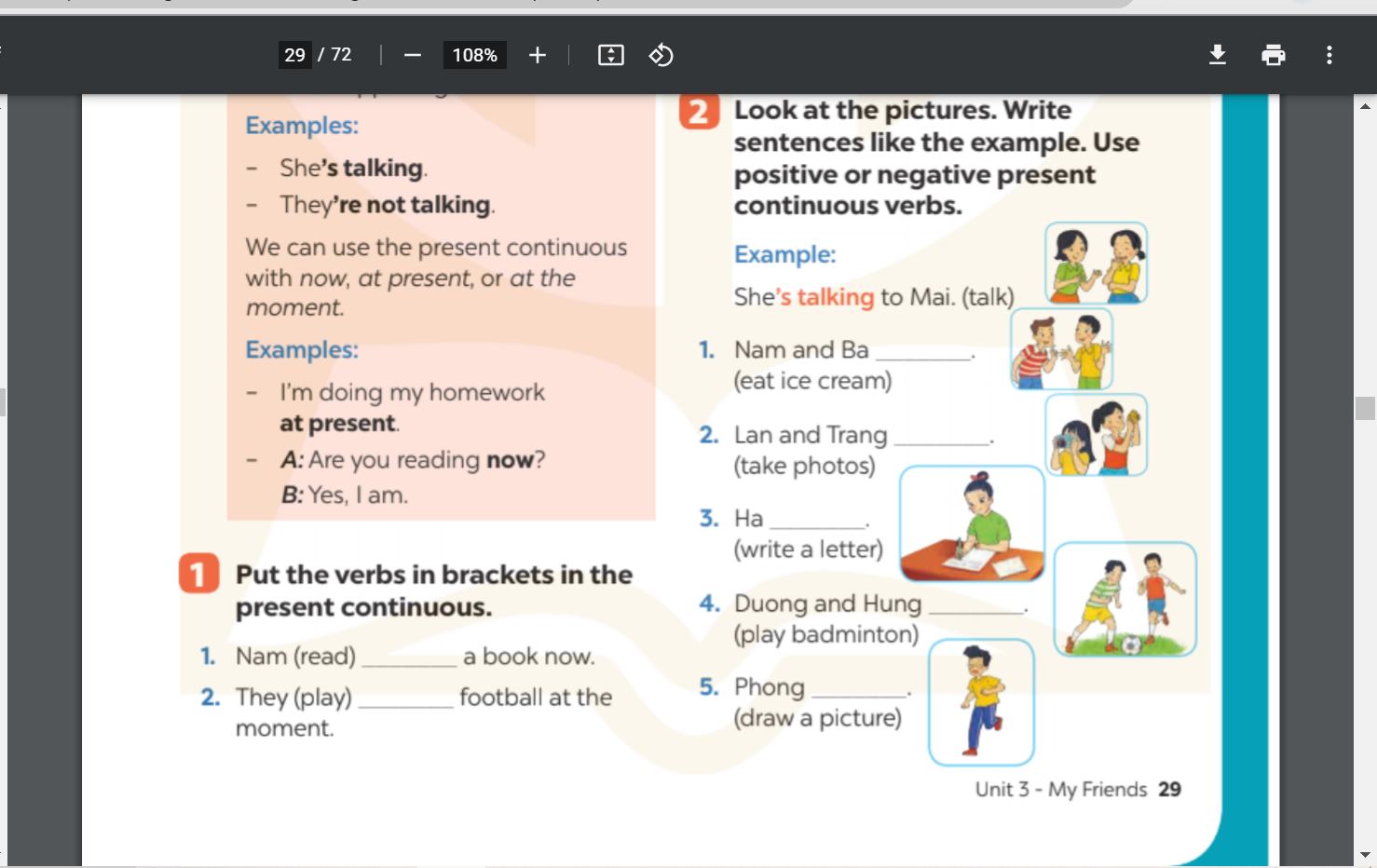
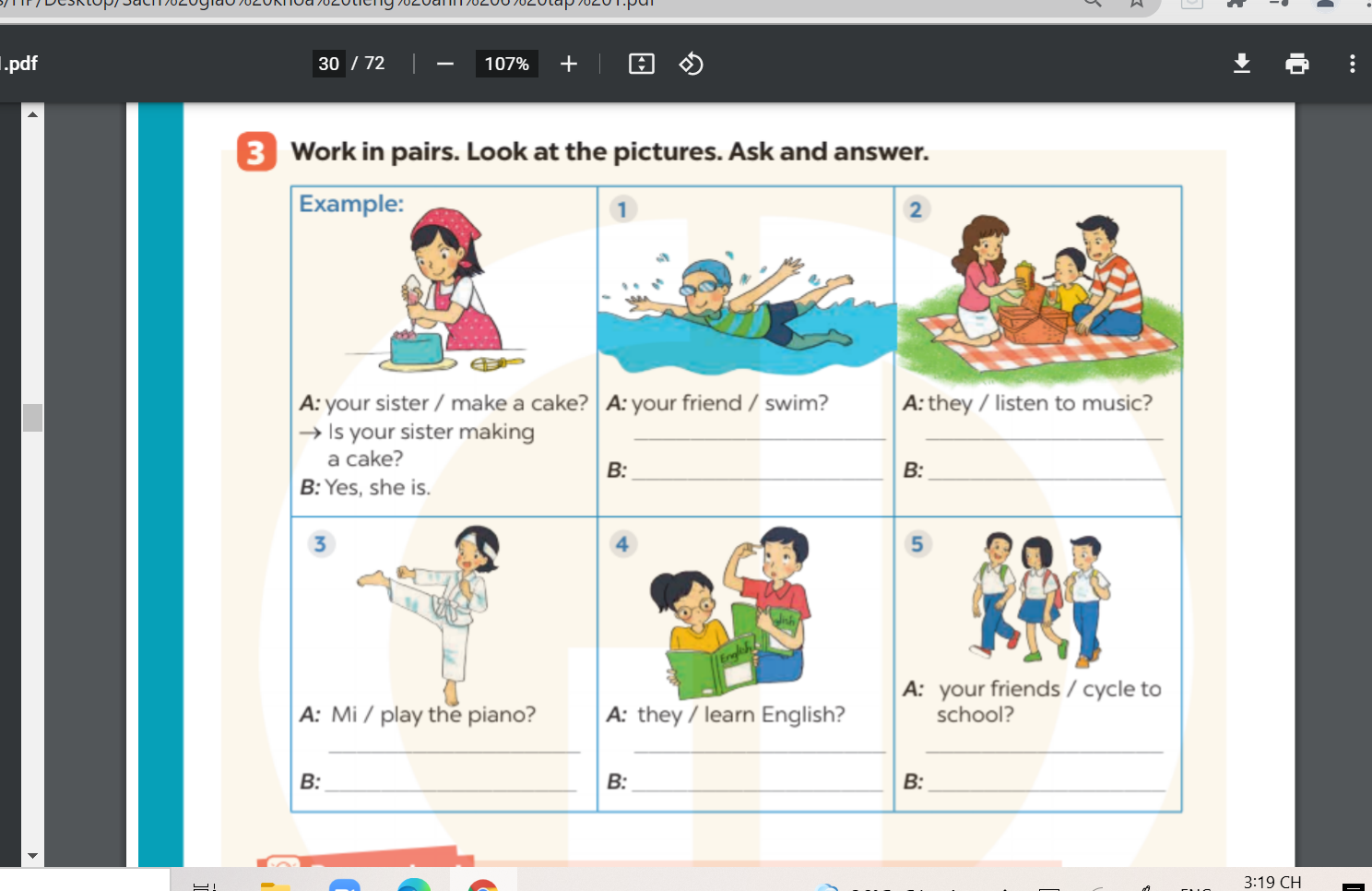
 các bn giúp mình bài 4, trang 30 hình ở trên ạ
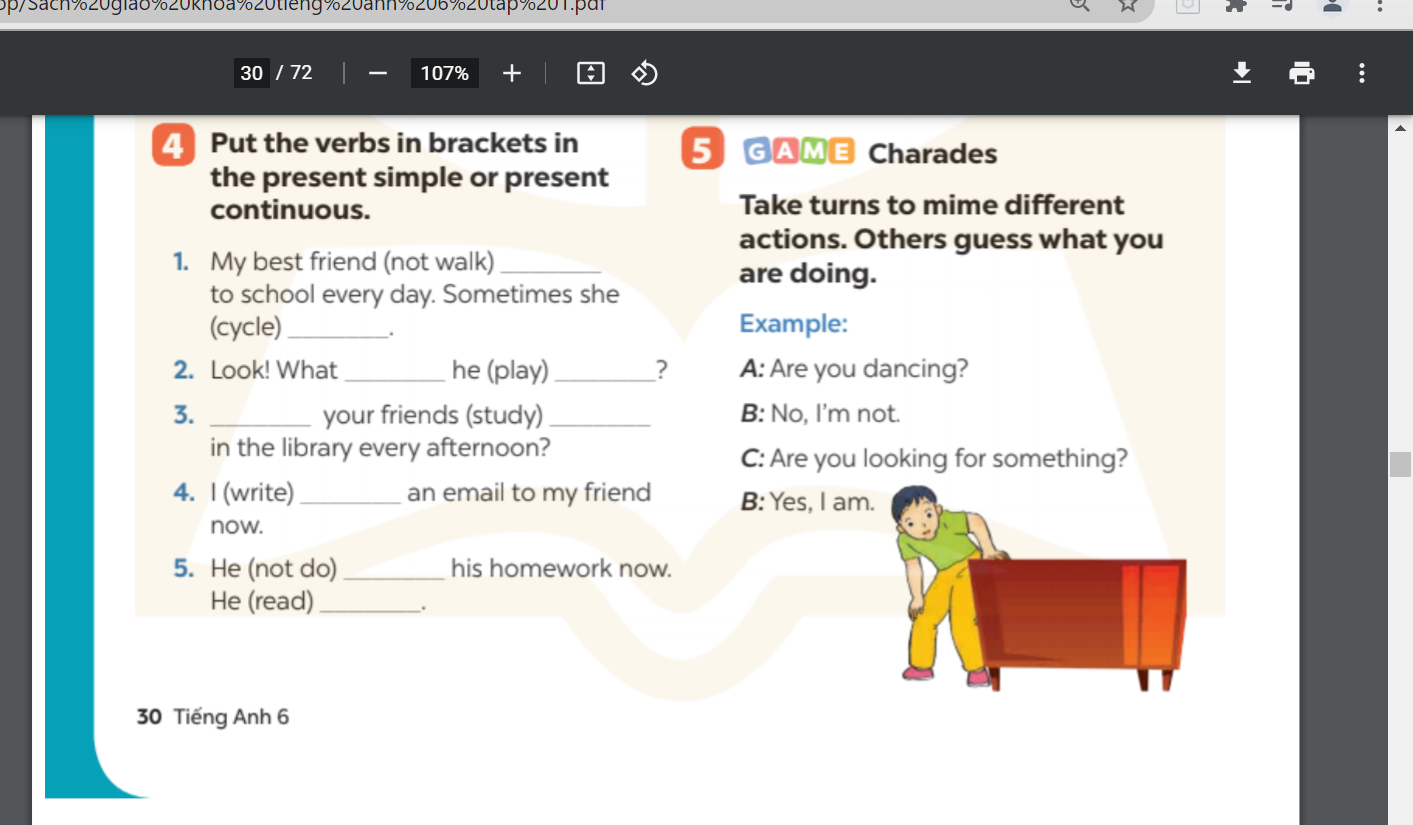
các bn giúp mình bài 4, trang 30 hình ở trên ạ bài 2, bài 3 ạ
bài 2, bài 3 ạ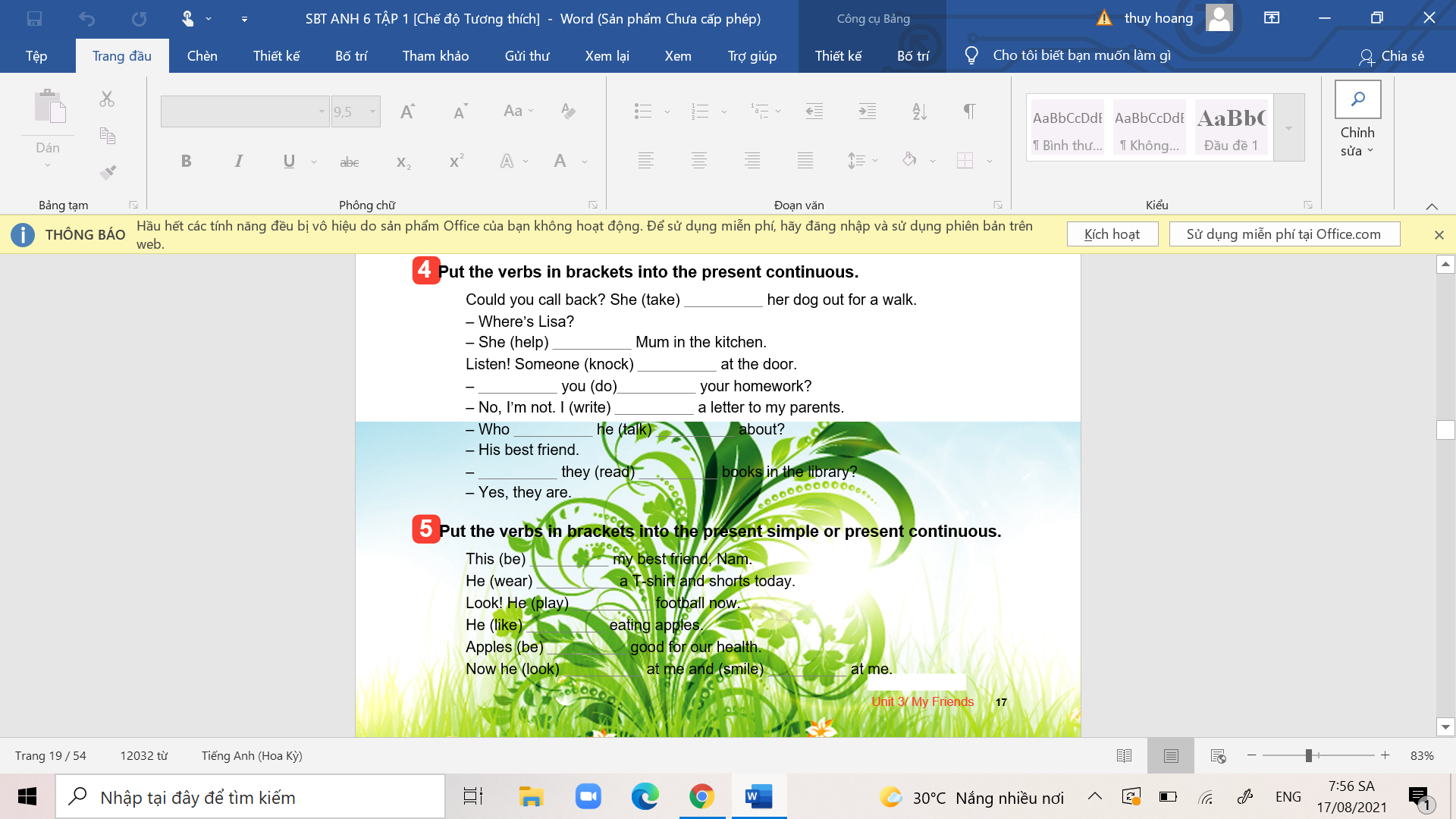




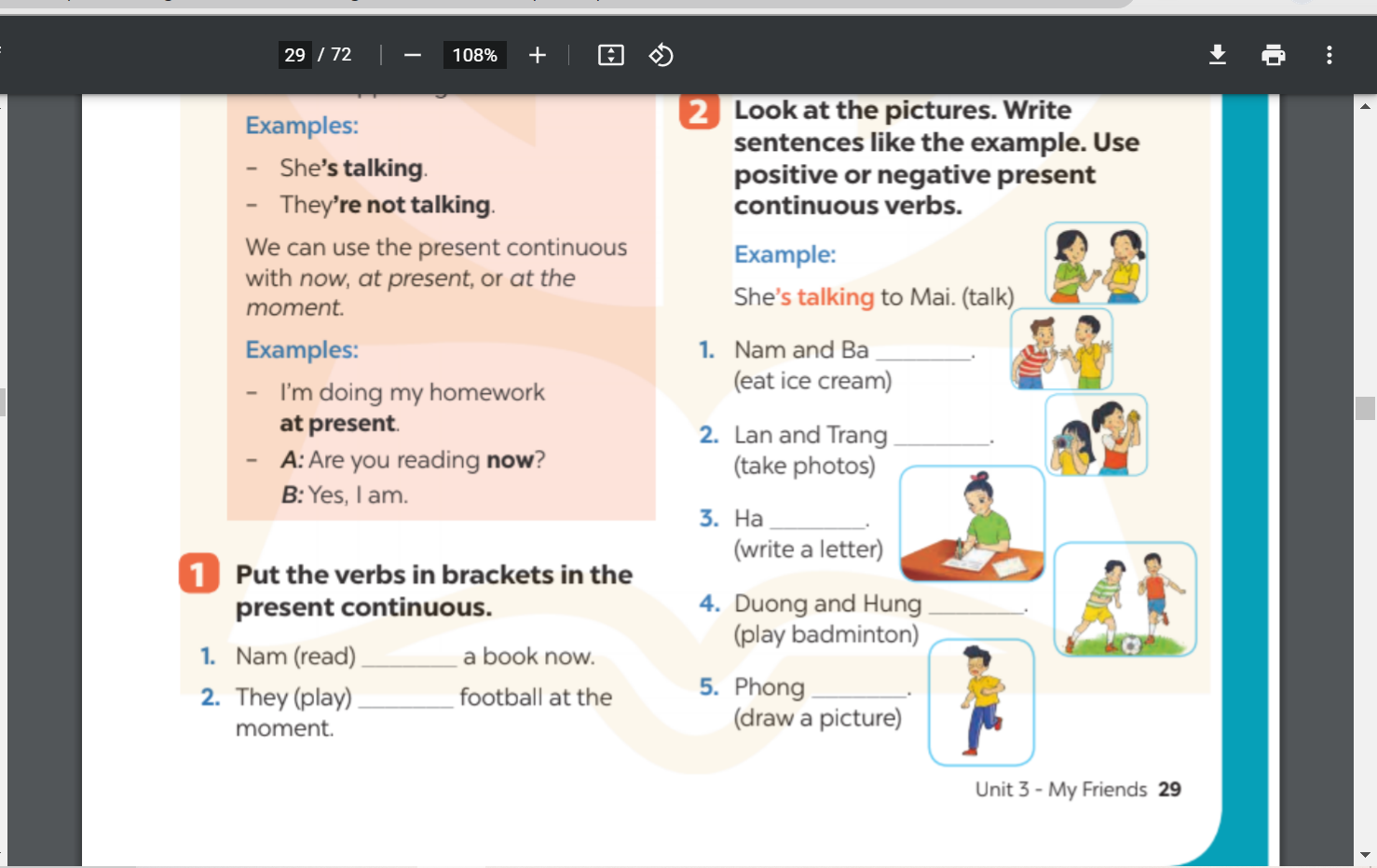 các bạn giúp mình bài 1, bài 2. trang 29 hình ở trên ạ
các bạn giúp mình bài 1, bài 2. trang 29 hình ở trên ạ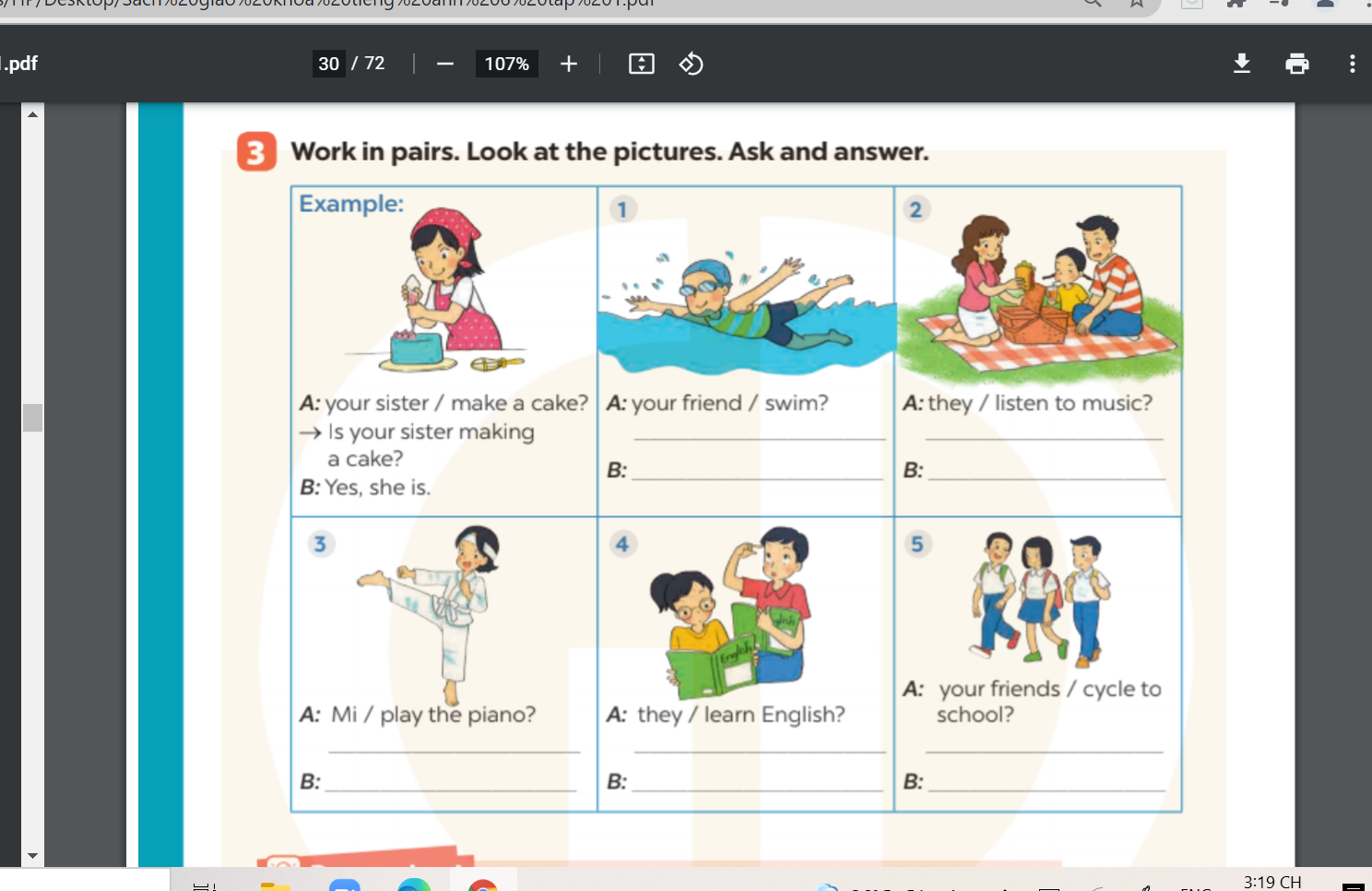 các bạn giúp mình bài 3 hình ở trên đó ạ
các bạn giúp mình bài 3 hình ở trên đó ạ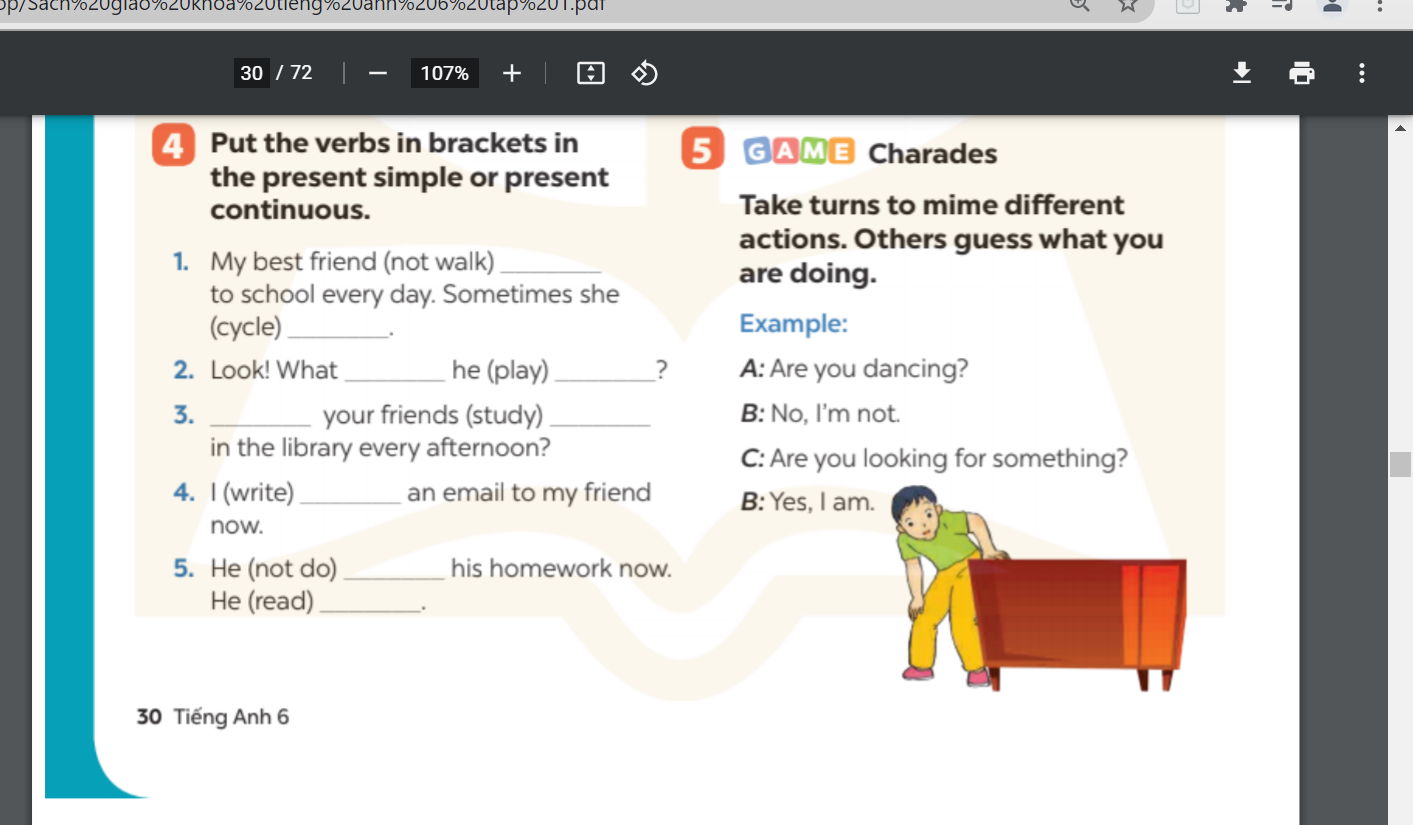

\(\lim\limits_{x\rightarrow4}\dfrac{2x-8}{4x^2-18x+8}=\lim\limits_{x\rightarrow4}\dfrac{2\left(x-4\right)}{2\left(x-4\right)\left(2x-1\right)}=\lim\limits_{x\rightarrow4}\dfrac{1}{2x-1}=-\dfrac{1}{7}\)
b.
\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt{x^2+3x-1}+x\right)=\lim\limits_{x\rightarrow-\infty}\dfrac{\left(\sqrt{x^2+3x-1}+x\right)\left(\sqrt{x^2+3x-1}-x\right)}{\sqrt{x^2+3x-1}-x}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{3x-1}{\sqrt{x^2+3x-1}-x}=\lim\limits_{x\rightarrow-\infty}\dfrac{3-\dfrac{1}{x}}{-\sqrt{1+\dfrac{3}{x}-\dfrac{1}{x^2}}-1}=\dfrac{3-0}{-\sqrt{1+0-0}-1}=-\dfrac{3}{2}\)
c.
\(\lim\limits_{x\rightarrow1^+}\dfrac{2x^2-3x+1}{x^2-1}=\lim\limits_{x\rightarrow1^+}\dfrac{\left(x-1\right)\left(2x-1\right)}{\left(x-1\right)\left(x+1\right)}=\lim\limits_{x\rightarrow1^+}\dfrac{2x-1}{x+1}=\dfrac{1}{2}\)
d.
\(\lim\limits_{x\rightarrow-\infty}\dfrac{2x^2+3x}{\sqrt{4x^4+2x^2}+3x^2-1}=\lim\limits_{x\rightarrow-\infty}\dfrac{x^2\left(2+\dfrac{3}{x}\right)}{x^2\left(\sqrt{4+\dfrac{2}{x^2}}+3-\dfrac{1}{x^2}\right)}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{2+\dfrac{3}{x}}{\sqrt{4+\dfrac{2}{x^2}}+3-\dfrac{1}{x^2}}=\dfrac{2+0}{\sqrt{4+0}+3-0}=\dfrac{2}{5}\)