Có hai con đường cắt nhau và cùng cắt một con sông tại hai điểm khác nhau hãy tìm một địa điểm để dựng một đài quan sát sao cho khoảng cách từ đó đến hai con đường và đến bờ sông bằng nhau
Có tất cả mấy điểm như vậy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai con đường cắt nhau và cùng cắt một con sông tạo thành tam giác ABC.
Vì khoảng cách từ điểm cần xây đến hai con đường và bờ sông là như nhau nên địa điểm để xây dựng đài quan sát thỏa mãn đề bài có thể là
- TH1: giao điểm của ba đường phân giác trong của tam giác ABC.
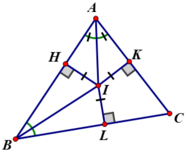
- TH2 : giao điểm M của hai tia phân giác ngoài và một tia phân giác trong. Ta có ba điểm M như vậy.
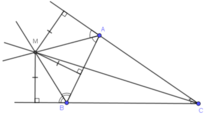
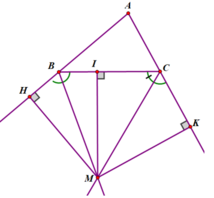
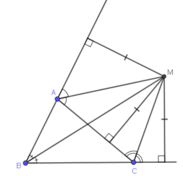
Vậy có tất cả 4 điểm có thể xây dựng đài quan sát thỏa mãn điều kiện.

Hướng dẫn:
Hai con đường cắt nhau và cùng cắt một con song tạo thành tam giác ABC. Địa điểm để xây dựng trạm kiểm lâm thỏa mãn đề bài phải là giao điểm I của ba đường phân giác trong của tam giác ABC và giao điểm K của tia phân giác của góc A và hai tia phân giác của các góc ngoài ở đỉnh D và đỉnh E của tam giác ADE.
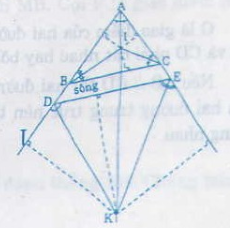
Vậy các địa điểm và các khoảng cách này ngắn nhất để xây dựng trạm kiểm lâm là I, K
Hai con đường cắt nhau và cùng cắt một con song tạo thành tam giác ABC. Địa điểm để xây dựng trạm kiểm lâm thỏa mãn đề bài phải là giao điểm I của ba đường phân giác trong của tam giác ABC và giao điểm K của tia phân giác của góc A và hai tia phân giác của các góc ngoài ở đỉnh D và đỉnh E của tam giác ADE.

Vậy các địa điểm và các khoảng cách này ngắn nhất để xây dựng trạm kiểm lâm là I, K

Gọi đường thẳng xy là bờ sông cần xây trạm bơm.
⇒ Bài toán đưa về: Hai điểm A, B cố định cùng nằm trên nửa mặt phẳng bờ là đường thẳng xy. Tìm vị trí điểm C nằm trên đường xy sao cho CA + CB nhỏ nhất.
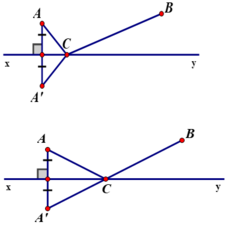
Gọi A’ là điểm đối xứng của A qua đường thẳng xy.
Theo như chứng minh ở bài 48 ta có: CA + CB = CA’ + CB ≥ A’B (A’B cố định).
⇒ CA + CB đạt ngắn nhất bằng A’B.
Dấu “=” xảy ra khi CA’+CB = A’B, tức là A’; B; C thẳng hàng hay C là giao điểm của A’B và xy.
Vậy điểm đặt trạm bơm là giao điểm của đường thẳng xy với đường thẳng A’B, trong đó A’ là điểm đối xứng với A qua xy.

Gọi đường thẳng xy là bờ sông cần xây trạm bơm.
⇒ Bài toán đưa về: Hai điểm A, B cố định cùng nằm trên nửa mặt phẳng bờ là đường thẳng xy. Tìm vị trí điểm C nằm trên đường xy sao cho CA + CB nhỏ nhất.
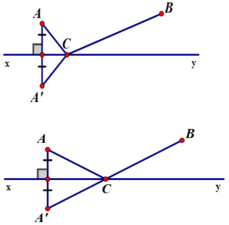
Gọi A’ là điểm đối xứng của A qua đường thẳng xy.
Theo như chứng minh ở bài 48 ta có: CA + CB = CA’ + CB ≥ A’B (A’B cố định).
⇒ CA + CB đạt ngắn nhất bằng A’B.
Dấu “=” xảy ra khi CA’+CB = A’B, tức là A’; B; C thẳng hàng hay C là giao điểm của A’B và xy.
Vậy điểm đặt trạm bơm là giao điểm của đường thẳng xy với đường thẳng A’B, trong đó A’ là điểm đối xứng với A qua xy.

Do hai con chim vồ mồi cùng 1 lúc và với cùng một vận tốc nên quãng đường bay của 2 con pải như nhau
Gọi khoảng cách của con cá tới 2 gốc cây lần lượt là x,y(x,y>0)
Khoảng cách bay của con 1 là : \(\sqrt{20^2+x^2}\)\
Khoảng cách bay của con thứ 2 là \(\sqrt{30^2+y^2}\)
Do khoảng cách bằng nhau nên ta có pt:
\(\sqrt{30^2+y^2}=\sqrt{20^2+x^2}\)
\(\Leftrightarrow500=x^2-y^2=\left(x+y\right)\left(x-y\right)\)
\(\Leftrightarrow500=50\left(x-y\right)\)(do x+y=50)
\(\Leftrightarrow x-y=10\)
\(\Rightarrow\hept{\begin{cases}x+y=50\\x-y=10\end{cases}\Rightarrow x=30,y=20}\)
Vậy con trên cây cao 30 m có gốc cây cách con cá 20m
con trên cây cao 20m có gốc cây cách con cá 30m

- Dựng điểm A' sao cho bờ sông là trung trực của AA'.
- Nối A'B cắt bờ sông tại điểm C.
Theo kết quả của bài 62 thì C là điểm cần tìm có khoảng cách CA + CB ngắn nhất.

Gọi đường thẳng xy là đường thẳng cần xây trạm bơm
Gọi A' là điểm đối xứng của A qua xy
Ta có: CA+CB=CA'+CB>=A'B
=>CA+CB ngắn nhất khi bằng A'B
Dấu '=' xảy ra khi C là giao điểm của AB và xy