cho nửa đường tròn o đường kính ab, 2 tia tiếp tuyến ax, by cùng thuộc 1 nửa mặt phẳng bờ ab có chứa nửa đường tròn. gọi o là 1 điểm nằm trên nửa đường tròn, qua m kẻ 1 đường thẳng vuông góc với cm cắ...

NT

Nguyễn Thị Tuyết Trâm

2 tháng 4 2017 - olm

cho nửa đường tròn o đường kính ab, 2 tia tiếp tuyến ax, by cùng thuộc 1 nửa mặt phẳng bờ ab có chứa nửa đường tròn. gọi o là 1 điểm nằm trên nửa đường tròn, qua m kẻ 1 đường thẳng vuông góc với cm cắt ã ở d, cắt by ở e a)cm: acmd, bcme nội tiếp b) am^2 = mk.mb c)so sánh góc mab, góc...

Đọc tiếp

#Toán lớp 9

0

SO

Scarlett Ohara

27 tháng 10 2021

Cho nửa đường tròn (O;R), có đường kính AB. Kẻ 2 tia Ax, By vuông góc AB (Ax, By, nửa đường tròn (O) cùng thuộc 1 nửa mặt phẳng bờ chứa AB). Trên nửa đường tròn lấy M (M khác A, B), qua M kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax, By theo thứ tự tại C, D.a, CM AC+BD=CD.b, CM góc COD = 90 độ.c, CM tích AC.BD không đổi khi M di chuyển trên nửa đường tròn.d, CB cắt DA tại K, MK cắt AB tại H. CM MK//AC//BD.e, CM K...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

27 tháng 10 2021

a: Xét (O) có

CM là tiếp tuyến có M là tiếp điểm

CA là tiếp tuyến có A là tiếp điểm

Do đó: CM=CA

Xét (O) có

DM là tiếp tuyến có M là tiếp điểm

DB là tiếp tuyến có B là tiếp điểm

Do đó: DM=DB

Ta có: CM+MD=CD

nên CD=CA+DB

Đúng(0)

SO

Scarlett Ohara

27 tháng 10 2021

mình cần phần d, f

Đúng(0)

TN

Thành Nhân Võ

15 tháng 12 2021

Cho nửa đường tròn (O;R), có đường kính AB. Kẻ hai tia Ax và By vuông góc với AB (Ax, By và nửa đường tròn (O) thuộc cùng một nửa mặt phẳng bờ chứa AB). Trên nửa đường tròn lấy điểm M (M khác A và B), qua M kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax và By theo thứ tự tại C và D.Chứng minh: a)AC + BD = CDb) (góc) COD = AC +...

Đọc tiếp

#Toán lớp 7

0

TM

Trần Mai Anh

25 tháng 12 2021

Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi C là 1 điểm bất kì trên nửa đường tròn ( C khác A,B ). qua C kẻ tiếp tuyến với nửa đường tròn cắt Ax, By tại M,N a. Tính MON b. Chứng minh rằng MN = AM + BN c. Chứng minh rằng AM.BN =...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

25 tháng 12 2021

b: Xét (O) có

MC là tiếp tuyến

MA là tiếp tuyến

Do đó: MC=MA

Xét (O) có

NC là tiếp tuyến

NB là tiếp tuyến

Do đó: NC=NB

Ta có: MN=MC+NC

nên MN=MA+NB

Đúng(0)

ND

Nguyễn Đình Long’s

4 tháng 7 2021

Cho nửa đường tròn (O) đường kính AB = a. Gọi Ax, By là các tia vuông góc với AB ( Ax, By thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (O) (M khác A và B) kẻ tiếp tuyến với nửa đường tròn (O); nó cắt Ax, By lần lượt ở E và F.1. Chứng minh: góc EOF = 90o2. Chứng minh tứ giác AEMO nội tiếp; hai tam giác MAB và OEF đồng dạng.3. Gọi K là giao điểm của AF và BE, chứng minh MK vuông góc...

Đọc tiếp

#Toán lớp 9

1

AT

An Thy

4 tháng 7 2021

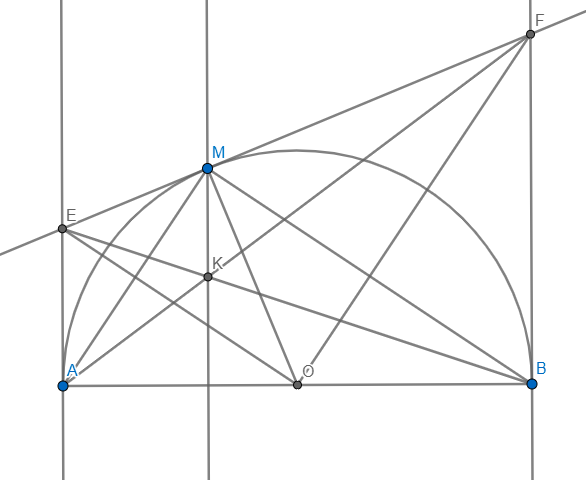
1) Vì EM,EA là tiếp tuyến \(\Rightarrow OE\) là phân giác \(\angle MOA\)

\(\Rightarrow\angle MOE=\dfrac{1}{2}\angle MOA\)

Vì FM,FB là tiếp tuyến \(\Rightarrow OF\) là phân giác \(\angle MOB\)

\(\Rightarrow\angle MOF=\dfrac{1}{2}\angle MOB\)

\(\Rightarrow\angle MOE+\angle MOF=\dfrac{1}{2}\left(\angle MOA+\angle MOB\right)=\dfrac{1}{2}.180=90\)

\(\Rightarrow\angle EOF=90\)

2) Ta có: \(\angle EAO+\angle EMO=90+90=180\Rightarrow AEMO\) nội tiếp

\(\Rightarrow\angle MEO=\angle MAO\)

Vì AB là đường kính \(\Rightarrow\angle AMB=90\)

Xét \(\Delta MAB\) và \(\Delta OEF:\) Ta có: \(\left\{{}\begin{matrix}\angle AMB=\angle EOF\\\angle FEO=\angle MAB\end{matrix}\right.\)

\(\Rightarrow\Delta MAB\sim\Delta OEF\left(g-g\right)\)

Vì \(AE\parallel BF(\bot AB)\) \(\Rightarrow\dfrac{BF}{AE}=\dfrac{FK}{AK}\left(1\right)\)

Vì EM,EA là tiếp tuyến \(\Rightarrow EA=EM\left(2\right)\)

Vì FM,FB là tiếp tuyến \(\Rightarrow FB=FM\left(3\right)\)

Thế (2),(3) vào (1) \(\Rightarrow\dfrac{FM}{EM}=\dfrac{FK}{AK}\Rightarrow\) \(MK\parallel AE\) \(\Rightarrow MK\bot AB\)

undefined

Đúng(1)

NM

Nott mee

13 tháng 12 2021

Cho nửa đường tròn (O) đường kính AB. Gọi Ax; By là các tia vuông góc với AB.(Ax ; By và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB).Qua điểm M thuộc nửa đường tròn ( M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax tại C và cắt By tại DA) c/m CD=AC+BD và COD = 90B) AD cắt BC tại N. Chứng minh: MN//BDC) Gọi H là trung điểm của AM. Chứng minh: ba điểm O, H , C thẳng hànggiúp tớ câu b và c...

Đọc tiếp

#Toán lớp 9

0

LP

Lợi Phan

8 tháng 10 2021

Cho nửa đường tròn tâm O, đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A,B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax và By theo thứ tự ở C và D. Biết CD=a và BD= 3ACa) CMR: OC và OD vuông gócb) Tính tỉ số AC^2+BD^2/ CD^2c) Tính theo a diện tích tứ giác...

Đọc tiếp

#Toán lớp 9

0

YN

Yến Nhi

15 tháng 12 2021

Bài 5. Cho nửa đường tròn (O) đường kính AB. Gọi Ax; By là các tia vuông góc với AB.(Ax ; By và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB).Qua điểm M thuộc nửa đường tròn ( M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax tại C và cắt By tại D.a) Chứng minh và b) AD cắt BC tại N. Chứng minh: c) Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn.d) Gọi H là trung...

Đọc tiếp

#Toán lớp 9

0

YN

Yến Nhi

14 tháng 12 2021

Bài 5. Cho nửa đường tròn (O) đường kính AB. Gọi Ax; By là các tia vuông góc với AB.(Ax ; By và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB).Qua điểm M thuộc nửa đường tròn ( M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax tại C và cắt By tại D.a) Chứng minh và b) AD cắt BC tại N. Chứng minh: c) Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn.d) Gọi H là trung...

Đọc tiếp

#Toán lớp 9

0

GF

Gãy Fan

20 tháng 1 2023

:. Cho nửa đường tròn (O), đường kính AB = 2R. Gọi Ax, By là các tia vuông góc với AB (Các tia Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm I thuộc nửa đường tròn (I khác A và B) kẻ tiếp tuyến với nửa đường tròn (O), nó cắt các tia Ax, By lần lượt ở M và N. a) Chứng minh:góc MON=90 độ b) Chứng minh : MN = AM + BN. c) Chứng minh AB là tiếp tuyến của đường tròn...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

20 tháng 1 2023

a: Xét (O) có

MI,MA là tiếp tuyến

nên MI=MA và OM là phân giác của góc AOI(1)

Xét (O) có

NI,NB là tiếp tuyến

nên NI=NB và ON là phân giác của góc IOB(2)

Từ (1), (2) suy ra góc MON=1/2*180=90 độ

b: MN=MI+IN

=>MN=MA+NB

c: Gọi H là trung điểm của MN

Xét hình thang AMNB có

O,H lần lượt là trung điểm của AB,MN

nên HO là đường trung bình

=>HO//AM//BN

=>HO vuông góc AB

=>AB là tiếp tuyến của(H)

Đúng(0)

C

caclodaisu

17 tháng 9 2021

Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc tia Ax. Qua M kẻ tiếp tuyến với nửa đường tròn, cắt By ở N.a. Tính số đo góc MONb. Chứng minh rằng MN = AM + BNc. Chứng minh rằng AM.BN = R2 (R là bán kính của nửa đường tròn)giúp với...

Đọc tiếp

#Toán lớp 9

1

NC

Nguyễn Cẩm Uyên

17 tháng 9 2021

bạn tự vẽ hình giúp mik nha

a) áp dụng t/c 2 tiếp tuyến cắt nhau ta có

OM là tia phân giác \(\widehat{AOI}\)

ON là tpg \(\widehat{IOB}\)

mà:\(\widehat{AOI}+\widehat{BOI}=180^o\)\(\Rightarrow OM\perp ON\)(t/c 2 góc kề bù)

vậy \(\widehat{MON}=90^o\)

b)từ t/c 2 tiếp tuyến cắt nhau ta có

MA=MI;BN=NI

\(\Rightarrow\)AM+BN=MI+NI=MN9(đpcm)

c)ta có:AM.BN=MI.NI(1)

xét \(\Delta MON\) vuông tại O có

MI.NI(đlý)=\(OI^2=R^2\)(2)

từ (1) và (2)\(\Rightarrow AM.BN=R^2\)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP