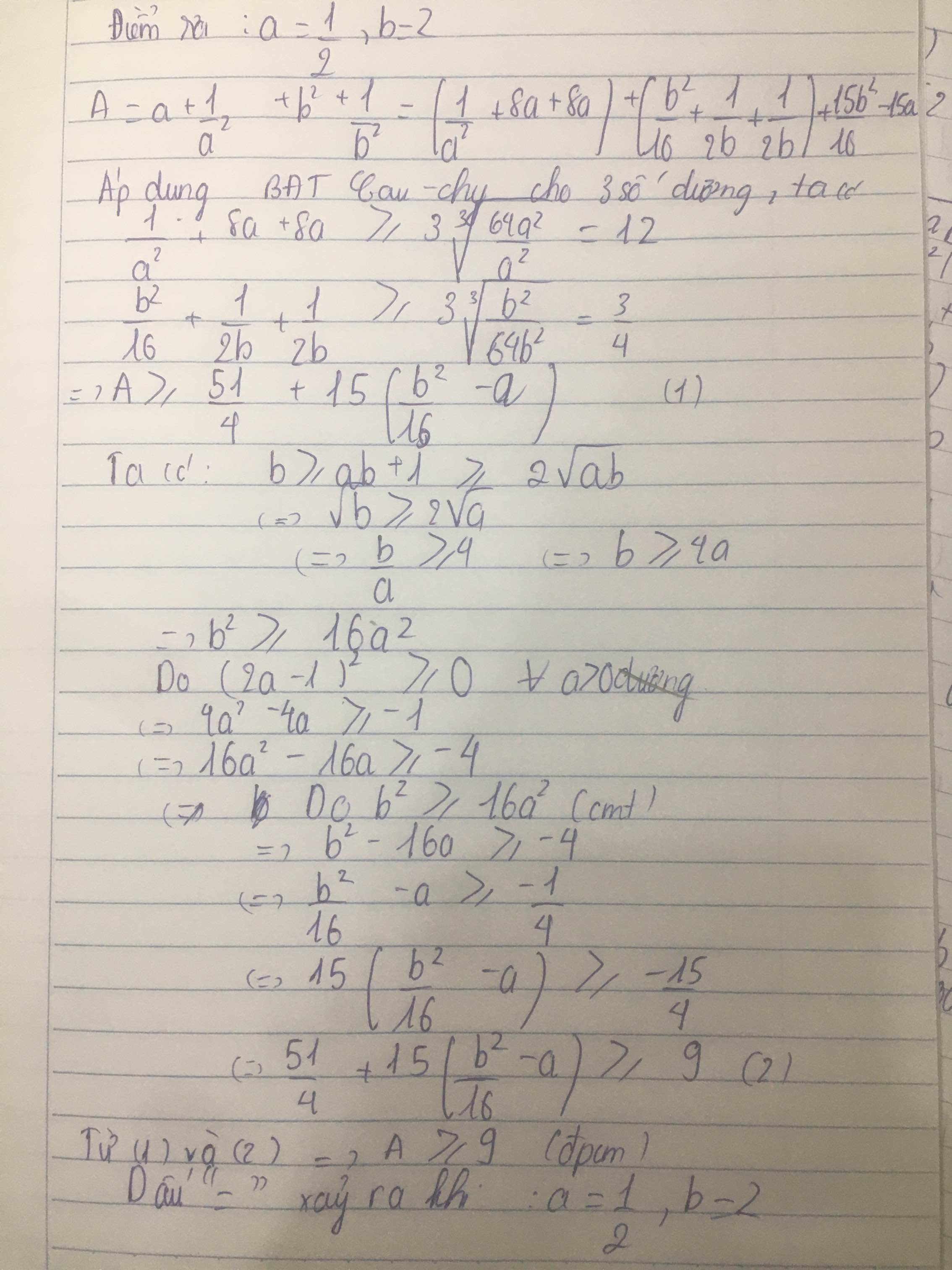cho a,b là 2 so dương thỏa mãn a^5+b^5=a^7+b^7 . Chứng minh a^2+b^2 nhỏ hơn hoặc bằng ab+1 .Dấu đẳng thức xảy ra khi nào?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HN
10 tháng 4 2017
\(a^2+b^2\le ab+1\)
\(\Leftrightarrow a^2-ab+b^2\le1\)
\(\Leftrightarrow\left(a+b\right)\left(a^2-ab+b^2\right)\le a+b\)
\(\Leftrightarrow a^3+b^3\le a+b\)
\(\Leftrightarrow\left(a^5+b^5\right)\left(a^3+b^3\right)\le\left(a^7+b^7\right)\left(a+b\right)\)
\(\Leftrightarrow ab^7+a^7b-a^3b^5-a^5b^3\ge0\)
\(\Leftrightarrow ab\left(b^6+a^6-a^2b^4-a^4b^2\right)\ge0\)
\(\Leftrightarrow ab\left(b-a\right)^2\left(b+a\right)^2\left(b^2+a^2\right)\ge0\) (đúng)
\(\RightarrowĐPCM\)
Dấu đẳng thức xảy ra khi ......
L
Cho a, b là 2 số dương. Chứng minh rằng: \(a^4+b^4\ge a^3b+ab^3\). Dấu của đẳng thức xảy ra khi nào?
0
KN
12 tháng 6 2020
Vì abc = 1 nên \(\frac{a}{ab+a+1}+\frac{b}{bc+b+1}+\frac{c}{ca+c+1}\)\(=\frac{ac}{abc+ac+c}+\frac{abc}{abc^2+abc+ac}+\frac{c}{ca+c+1}\)
\(=\frac{ac}{ac+c+1}+\frac{1}{ac+c+1}+\frac{c}{ac+c+1}=\frac{ac+c+1}{ac+c+1}=1\)(*)
Áp dụng bất đẳng thức Bunyakovsky dạng phân thức và áp dụng đẳng thức (*), ta được:
\(\frac{a}{\left(ab+a+1\right)^2}+\frac{b}{\left(bc+b+1\right)^2}+\frac{c}{\left(ca+c+1\right)^2}\)\(=\frac{\left(\frac{a}{ab+a+1}\right)^2}{a}+\frac{\left(\frac{b}{bc+b+1}\right)^2}{b}+\frac{\left(\frac{c}{ca+c+1}\right)^2}{c}\)
\(\ge\frac{\left(\frac{a}{ab+a+1}+\frac{b}{bc+b+1}+\frac{c}{ca+c+1}\right)^2}{a+b+c}=\frac{1}{a+b+c}\)
Đẳng thức xảy ra khi a = b = c = 1
22 tháng 3 2021
1) a2 - ab + b2 ≥ 0
<=> ( 4a2 - 4ab + b2 ) + 3b2 ≥ 0
<=> ( 2a - b )2 + 3b2 ≥ 0 ( đúng ∀ a,b )
Vậy bđt ban đầu được chứng minh
Đẳng thức xảy ra <=> a = b = 0
2) a2 - ab + b2 ≥ 1/4( a + b )2
<=> 4a2 - 4ab + 4b2 ≥ a2 + 2ab + b2
<=> 4a2 - 4ab + 4b - a2 - 2ab - b2 ≥ 0
<=> 3a2 - 6ab + 3b2 ≥ 0
<=> a2 - 2ab + b2 ≥ 0
<=> ( a - b )2 ≥ 0 ( đúng ∀ a,b )
Vậy bđt ban đầu được chứng minh
Đẳng thức xảy ra <=> a = b
S
23 tháng 5 2017
\(VT=\sqrt{\frac{ab}{\left(a+c\right)\left(b+c\right)}}+\sqrt{\frac{bc}{\left(a+b\right)\left(a+c\right)}}+\sqrt{\frac{ca}{\left(b+c\right)\left(a+b\right)}}\)
Áp dụng bất đẳng thức Cauchy - Schwarz
\(\Rightarrow\sqrt{\frac{ab}{\left(a+c\right)\left(b+c\right)}}\le\frac{\frac{a}{a+c}+\frac{b}{b+c}}{2}\)
Tượng tự ta có \(\hept{\begin{cases}\sqrt{\frac{bc}{\left(a+b\right)\left(a+c\right)}}\le\frac{\frac{b}{a+b}+\frac{c}{a+c}}{2}\\\sqrt{\frac{ca}{\left(b+c\right)\left(a+b\right)}}\le\frac{\frac{c}{b+c}+\frac{a}{a+b}}{2}\end{cases}}\)
\(\Rightarrow VT\le\frac{\left(\frac{a}{a+b}+\frac{b}{a+b}\right)+\left(\frac{c}{a+c}+\frac{a}{c+a}\right)+\left(\frac{c}{b+c}+\frac{b}{c+b}\right)}{2}\)
\(\Rightarrow VT\le\frac{\frac{a+b}{a+b}+\frac{c+a}{c+a}+\frac{b+c}{b+c}}{2}=\frac{3}{2}\) ( đpcm )
Dấu " = " xảy ra khi \(a=b=c=\frac{1}{3}\)
C6. Cho các số thực dương thoả mãn: ab+1 nhỏ hơn hoặc bằng b Chứng minh rằng : ( a + (1/a^2) ) + ( b^2 + (1/b) ) lớn hơn hoặc bằng 9
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2022
\(ab+1\le b\Rightarrow a+\dfrac{1}{b}\le1\)
Đặt \(\left(a;\dfrac{1}{b}\right)=\left(x;y\right)\Rightarrow x+y\le1\)
Gọi vế trái của BĐT cần chứng minh là P:
\(P=x+\dfrac{1}{x^2}+y+\dfrac{1}{y^2}=\left(\dfrac{1}{x^2}+8x+8x\right)+\left(\dfrac{1}{y^2}+8y+8y\right)-15\left(x+y\right)\)
\(P\ge3\sqrt[3]{\dfrac{64x^2}{x^2}}+3\sqrt[3]{\dfrac{64y^2}{y^2}}-15.1=9\) (đpcm)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(\dfrac{1}{2};\dfrac{1}{2}\right)\) hay \(\left(a;b\right)=\left(\dfrac{1}{2};2\right)\)
CW
15 tháng 3 2018
lần đầu tự làm được 1 bài bđt theo kiểu nháp phát đc liền... hp quớ ~~~
Đặt A = VT
từ giả thiết, ta suy ra:
\(A=\dfrac{b+c+a+b+c-2}{2+a}+\dfrac{c+a+a+b+c-3}{3+b}+\dfrac{a+b+a+b+c-4}{4+c}\)
\(=\dfrac{2\left(a+b+c\right)-2-a}{2+a}+\dfrac{2\left(a+b+c\right)-3-b}{3+b}+\dfrac{2\left(a+b+c\right)-4-c}{4+c}\)
\(=2\left(a+b+c\right)\left(\dfrac{1}{2+a}+\dfrac{1}{3+b}+\dfrac{1}{4+c}\right)-3\)
\(=18\left(\dfrac{1}{2+a}+\dfrac{1}{3+b}+\dfrac{1}{4+c}\right)-3\)
Đặt \(B=\dfrac{1}{2+a}+\dfrac{1}{3+b}+\dfrac{1}{4+c}\)
Áp dụng bđt schwarz cho các số thực không âm:
\(B\ge\dfrac{9}{a+b+c+9}=\dfrac{1}{2}\)
vậy \(A\ge18\cdot B-3=18\cdot\dfrac{1}{2}-3=6\left(đpcm\right)\)
dấu "=" xảy ra khi \(\dfrac{1}{2+a}=\dfrac{1}{3+b}=\dfrac{1}{4+c}=\dfrac{1}{6}\) \(\Leftrightarrow\left\{{}\begin{matrix}a=4\\b=3\\c=2\end{matrix}\right.\)