Cho ABC nhọn có 0 A = 60 ˆ , các đường cao là BE và CF. Chứng minh: ABC ~ AEF và SABC = 4SAEF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


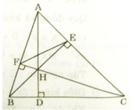
a) Xét ΔAEB và ΔAFC có:
∠AEB = ∠AFC = 90o (gt)
∠A chung
Vậy ΔAEB ∼ ΔAFC (g.g)
![]()
b) Xét ΔAEF và ΔABC có
∠A chung
AF.AB = AE.AC (Cmt)
⇒ ΔAEF ∼ ΔABC (c.g.c)
⇒ ∠AEF = ∠ABC
c) ΔAEF ∼ ΔABC (cmt)

![]()
![]()
![]()
![]()
![]()
![]()
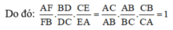

a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc A chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF
b: AE/AF=AB/AC
=>AE/AB=AF/AC
=>ΔAEF đồng dạng với ΔABC
=>góc AEF=góc ABC
c: ΔAEF đồng dạng với ΔABC
=>\(\dfrac{S_{AEF}}{S_{ABC}}=\dfrac{1}{4}\)
=>\(S_{ABC}=4\cdot S_{AEF}\)

a) Xét \(\Delta AEB\) và \(\Delta AFC\) có:
\(\widehat{AEB}=\widehat{AFC}=90^0\)
\(\widehat{A}\) chung
suy ra: \(\Delta AEB~\Delta AFC\) (g.g)
\(\Rightarrow\)\(\frac{AE}{AF}=\frac{AB}{AC}\) \(\Rightarrow\)\(AF.AB=AE.AC\)
b) \(\frac{AE}{AF}=\frac{AB}{AC}\)\(\Rightarrow\)\(\frac{AE}{AB}=\frac{AF}{AC}\)
Xét \(\Delta AEF\)và \(\Delta ABC\) có:
\(\frac{AE}{AB}=\frac{AF}{AC}\) (cmt)
\(\widehat{A}\) chung
suy ra: \(\Delta AEF~\Delta ABC\) (c.g.c)
\(\Rightarrow\) \(\widehat{AEF}=\widehat{ABC}\)
c) \(\Delta AEF~\Delta ABC\)
\(\Rightarrow\)\(\frac{S_{ABC}}{S_{AEF}}=\left(\frac{AB}{AE}\right)^2=\left(\frac{3}{6}\right)^2=\frac{1}{4}\)
\(\Rightarrow\)\(S_{ABC}=4S_{AEF}\)
Gửi các bạn lời giải 1 bài tương tự
https://youtu.be/mjiZSkISHgA

Xét tam giác AEF và tam giác ABC có:
A chung
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\left(=cosA\right)\)
\(\Rightarrow\Delta AEF\sim\Delta ABC\left(c.g.c\right)\)
\(\Rightarrow\dfrac{S_{AEF}}{S_{ABC}}=\left(\dfrac{AE}{AB}\right)^2=cos^2A=1-sin^2A\)
\(1-\sin^2A=\cos^2A=\dfrac{AF^2}{AC^2}\left(1\right)\)
Ta có \(\widehat{AEB}=\widehat{AFC}=90^0\Rightarrow\Delta AEB\sim\Delta AFC\left(g.g\right)\)
\(\Rightarrow\dfrac{AE}{AB}=\dfrac{AF}{AC}\Rightarrow\Delta AEF\sim\Delta ABC\left(c.g.c\right)\\ \Rightarrow\dfrac{S_{AEF}}{S_{ABC}}=\left(\dfrac{AF}{AC}\right)^2=\dfrac{AF^2}{AC^2}\left(2\right)\\ \left(1\right)\left(2\right)\RightarrowĐpcm\)

a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc EAB chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF;AE/AB=AF/AC
b: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc A chung
=>ΔAEF đồng dạng vói ΔABC
=>\(\dfrac{S_{AEF}}{S_{ABC}}=\left(\dfrac{AE}{AB}\right)^2=\dfrac{1}{4}\)
=>\(S_{ABC}=4\cdot S_{AEF}\)

b) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{BAE}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC(g-g
Suy ra: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
hay \(AF\cdot AB=AE\cdot AC\)
c: Ta có: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
nên \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
\(\widehat{FAE}\) chung
Do đó: ΔAEF\(\sim\)ΔABC(c-g-c)

hứng minh được , từ đó có .AE phần AB=AF phần AC
Ta có: (g.c.g)
b, từ câu a) suy ra EF phần BC=AE phần AB=cos A=cos60 độ =1 phần 2
=> BC=10cm
c) Saef phần Sabc=(AE phần AB)^2=cos^2 A=1 phần 4 => SAEF =1 phần 4 SABC=25cm^2

\(7,\)
\(a,\left\{{}\begin{matrix}AB=AC\left(\Delta ABC.cân\right)\\\widehat{B_1}=\widehat{C_1}\left(\dfrac{1}{2}\widehat{ABC}=\dfrac{1}{2}\widehat{ACB}\right)\\\widehat{BAC}.chung\end{matrix}\right.\Rightarrow\Delta AFC=\Delta AEB\left(g.c.g\right)\\ \Rightarrow AF=AE\Rightarrow\Delta AFE.cân.tại.A\)
\(b,\left\{{}\begin{matrix}\widehat{ABC}=\widehat{ACB}\left(\Delta ABC.cân\right)\\BC.chung\\\widehat{B_2}=\widehat{C_2}\left(\dfrac{1}{2}\widehat{ABC}=\dfrac{1}{2}\widehat{ACB}\right)\end{matrix}\right.\Rightarrow\Delta BFC=\Delta CEB\left(g.c.g\right)\)
\(c,\widehat{F_1}=\dfrac{180^0-\widehat{BAC}}{2}\left(\Delta AEF.cân\right);\widehat{ABC}=\dfrac{180^0-\widehat{BAC}}{2}\left(\Delta ABC.cân\right)\\ \Rightarrow\widehat{F_1}=\widehat{ABC}\)
Mà 2 góc này ở vị trí đồng vị nên \(EF//BC\Rightarrow BEFC\) là hình thang
Mà \(\widehat{ABC}=\widehat{ACB}\left(GT\right)\)
Vậy \(BEFC\) là hình thang cân



góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc AFE=góc ACB
=>ΔAFE đồng dạng với ΔACB
=>\(\dfrac{S_{ABC}}{S_{AEF}}=\left(\dfrac{AB}{AE}\right)^2=4\)
=>\(S_{ABC}=4\cdot S_{AEF}\)