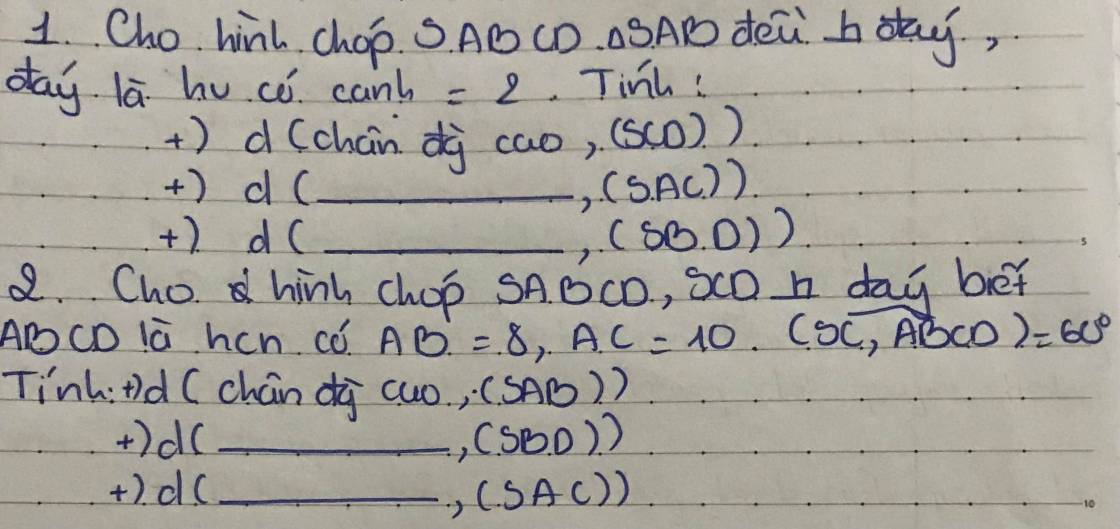 Giúp e vs ạ e cần gấp
Giúp e vs ạ e cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

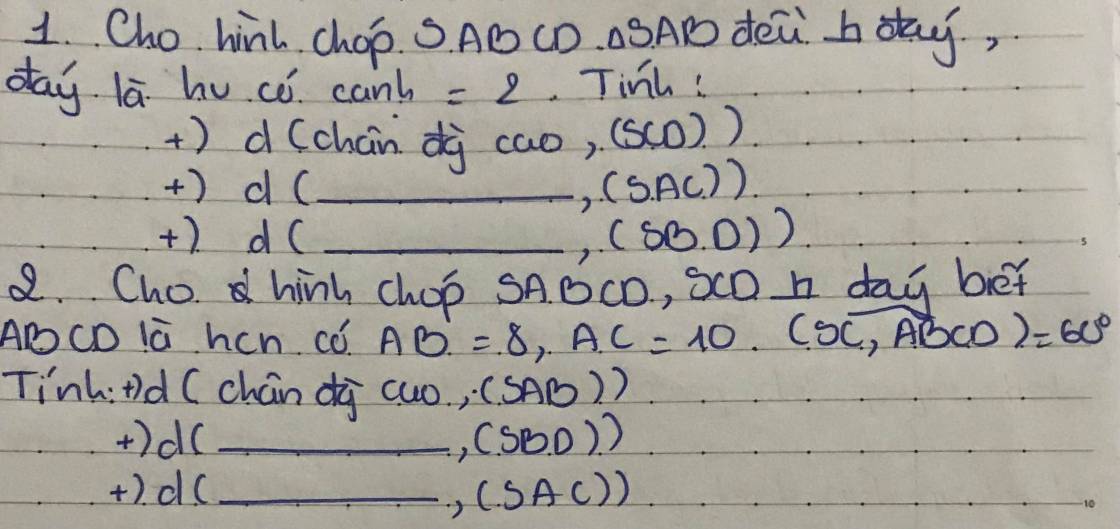

g: \(=\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\)
h: \(=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
\(e,=\dfrac{1}{x-1}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x^2-2x+1}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{\left(x-1\right)^2}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x-1}{x^2+1}\\ f,=\dfrac{3x-1}{2\left(3x+1\right)}+\dfrac{3x+1}{2\left(3x-1\right)}-\dfrac{6x}{\left(3x-1\right)\left(3x+1\right)}\\ =\dfrac{9x^2-6x+1+9x^2+6x+1-12x}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{2\left(3x-1\right)^2}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{3x-1}{3x+1}\)
\(g,=\dfrac{x}{x\left(x-2\right)}-\dfrac{x^2+4x}{x\left(x-2\right)\left(x+2\right)}-\dfrac{2}{x\left(x+2\right)}\\ =\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\\ h,=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)

`2)`
`@` Xét `3x+6 >= 0<=>x >= -2`
`=>A=[-2;+oo)`
`@` Xét `|x-2| < 3`
`<=>-3 < x-2 < 3`
`<=>-1 < x < 5=>B=(-1;5)`
Có: `A nn B=(-1;5)`
`A uu B=[-2;+oo)`
`R \\ B=(-oo;-1]uu[5;+oo)`
_______
`3)`
`@` Xét `x+3 >= 2x+7<=>x <= -4=>A=(-oo;-4]`
`@` Xét `4x+5 > 0<=>x > -5/4=>B=(-5/4;+oo)`
`@` Xét `|x+4| < 2<=>-2 < x+4 < 2<=>-6 < x < -2 =>C=(-6;-2)`
Có: `A nn B nn C=\emptyset`
`A \\ B nn C=(-6;-4]`
`C \\ A nn B=\emptyset`.

Bài 4:
Theo định lý sin ta có:
\(\dfrac{AC}{sinB}=\dfrac{BC}{sinA}\)
\(\Rightarrow BC=a=\dfrac{b\cdot sinA}{sinB}=\dfrac{2\cdot sin60^o}{sin45^o}=\sqrt{6}\)
\(\Rightarrow\widehat{C}=180^o-60^o-45^o=75^o\)
\(\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
\(\Rightarrow AB=c=\dfrac{b\cdot sinC}{sinB}=\dfrac{2\cdot sin75^o}{sin45^o}=1+\sqrt{3}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AC\cdot AB\cdot sinA=\dfrac{1}{2}\cdot2\cdot\left(1+\sqrt{3}\right)\cdot sin75^o=\dfrac{\sqrt{6}+2\sqrt{2}}{2}\) (đvdt)
Bán kình hình tròn tam giác ABC khi đó là:
\(S_{ABC}=\dfrac{abc}{4R}\)
\(\Rightarrow R=\dfrac{abc}{4S_{ABC}}=\dfrac{2\cdot\left(1+\sqrt{3}\right)\cdot\sqrt{6}}{4\cdot\left(\dfrac{\sqrt{6}+2\sqrt{2}}{2}\right)}=3-\sqrt{3}\)
Bài 3:
a) Xét tam giác ABC theo định lý côsin ta có:
\(cosC=\dfrac{a^2+b^2-c^2}{2ab}=\dfrac{8^2+10^2-13^2}{2\cdot8\cdot10}=-0,03125\)
\(\Rightarrow\widehat{C}=cos^{-1}-0,03125\approx91^o>90^o\)
Nên tam giác ABC có góc C là góc tù
c) Theo hệ thức Heron ta có diện tích tam giác ABC là:
\(S_{ABC}=\sqrt{p\cdot\left(p-a\right)\cdot\left(p-b\right)\cdot\left(p-c\right)}\)
\(\Rightarrow S_{ABC}=\sqrt{\dfrac{8+10+13}{2}\cdot\left(\dfrac{8+10+13}{2}-8\right)\cdot\left(\dfrac{8+10+13}{2}-10\right)\cdot\left(\dfrac{8+10+13}{2}-13\right)}\)
\(\Rightarrow S_{ABC}\approx40\) (đvdt)
b) Bán kính đường tròn ngoại tiếp tam giác ABC là:
\(S_{ABC}=\dfrac{abc}{4R}\)
\(\Rightarrow R=\dfrac{abc}{4S_{ABC}}=\dfrac{8\cdot10\cdot13}{4\cdot40}=6,5\)


Bài I
\(1,=x\left(x-y\right)\\ 2,=x\left(y+1\right)+y+1=\left(x+1\right)\left(y+1\right)\\ 3,=x\left(x^2-2x-5x+10\right)=x\left(x-2\right)\left(x-5\right)\)
Bài II
\(1,=x-x^2+x^2-x-2=-2\\ 2,\Leftrightarrow x^2+6x+9-x^2=45\\ \Leftrightarrow6x=36\Leftrightarrow x=6\)
Bài III
\(1,A=\dfrac{4-9}{3\left(2+5\right)}=\dfrac{-5}{3\cdot7}=-\dfrac{5}{21}\\ 2,B=\dfrac{x^2-3x+2x^2+6x-3x^2-9}{\left(x-3\right)\left(x+3\right)}=\dfrac{3\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{3}{x+3}\\ 3,P=AB=\dfrac{\left(x-3\right)\left(x+3\right)}{3\left(x+5\right)}\cdot\dfrac{3}{x+3}=\dfrac{x-3}{x+5}=1-\dfrac{8}{x+5}\in Z\\ \Leftrightarrow x+5\inƯ\left(8\right)=\left\{-8;-4;-2;-1;1;2;4;8\right\}\\ \Leftrightarrow x\in\left\{-13;-9;-7;-6;-4;-1;3\right\}\)