Phòng họp có 360 ghế xếp vào các dãy ghế. Trong một lần họp phải xếp thêm một dãy ghế, mỗi dãy tăng 1 ghế để đủ 450 đại biểu. Tìm dãy ghế lúc đầu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (dãy) là số dãy ghế ban đầu của phòng họp.
Điều kiện: x ∈N*
Khi đó số ghế ngồi trong một dãy là: 360/x (ghế)
số dãy ghế sau khi tăng là x + 1 (dãy)
số ghế ngồi trong một dãy sau khi tăng là: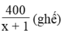
Theo đề bài, ta có phương trình: ![]()
⇔ 400x – 360(x + 1) = x(x + 1)
⇔ 400x – 360x – 360 = x 2 + x ⇔ x 2 – 39x + 360 = 0
∆ = - 39 2 – 4.1.360 = 1521 – 1440 = 81 > 0
∆ = 81 = 9
![]()
Cả hai giá trị của x đều thỏa mãn điều kiện bài toán.
Vậy bình thường trong phòng có 15 hoặc 24 dãy ghế.

Gọi số ghế ở mỗi hàng ban đầu là x (ghế, x > 0)
Gọi số hàng ghế trong phòng ban đầu là y (hàng, y < 50)
Ta có x nhân y = 240
Khi tăng số ghế và số hàng ta có (x + 1)(y + 3)= 315
Ta có hệ phương trình {x nhân y= 240
{y + 3x = 72
Giải hệ phương trình ta có y= 12; x= 20
Vậy số dãy ghế có trong phòng lúc đầu là 12 hàng.

Gọi số ghế ở mỗi hàng ban đầu là x (ghế, x > 0)
Gọi số hàng ghế trong phòng ban đầu là y (hàng, y < 50)
Ta có x nhân y = 240
Khi tăng số ghế và số hàng ta có (x + 1)(y + 3)= 315
Ta có hệ phương trình {x nhân y= 240
{y + 3x = 72
Giải hệ phương trình ta có y= 12; x= 20
Vậy số dãy ghế có trong phòng lúc đầu là 12 hàng.

Gọi số dãy ghế có trong phòng họp lúc đầu là x (x<50)
Lúc đầu mỗi dãy có \(\frac{240}{x}\)ghế
Vì lúc sau có 315 người tham dự nên phải kê thêm 3 dãy, mỗi dãy thêm 1 ghế
=> \(\left(\frac{240}{x}+1\right)\left(x+3\right)=315\Leftrightarrow240+\frac{720}{x}+x+3=315\)
\(\Leftrightarrow x-72+\frac{720}{x}=0\Leftrightarrow\frac{x^2-72x+720}{x}=0\Leftrightarrow x^2-72x+720=0\)
\(\Delta'=\left(-36\right)^2-720=576\)
=> x1= 60 (Loại), x2=12 (thỏa mãn)
Vậy trong phòng họp lúc đầu có 12 dãy ghế.

Gọi số dãy ghế ban đầu là a [a>0 ,a thuộc N]
=>Số người trên mỗi dãy ghế là : \(\frac{70}{a}\)
Khi bớt đi 2 dãy ghế => Số dãy ghế còn lại là : a-2
Số người trên mỗi dãy ghế lúc đó là : \(\frac{70}{a-2}\)
Theo bài ra ta có : \(\frac{70}{a}+4=\frac{70}{a-2}\)
=> 70[a-2]+4a[a-2]=70a =>35[a-2]+2a[a-2]=35a
=> 35a-70+2a\(^2\)-4a=35a
=> 2a\(^2\)-4a-70=0
=> \(a^2-2a-35=0=>a^2-2a+1-36=0=>\left[a-1^2\right]=36=6^2\). Có 2 trường hợp
Trường hợp 1 : a-1 = -6 => a = - 5 [loại]
Trường hợp 2 : a - 1 = 6 => a = 7
Còn đây bạn làm nốt tiếp
Vậy phòng họp lúc đầu có 7 dãy ghế và 10 người

Gọi số dãy là x, số người ngồi trong mỗi dãy là y dk:...
Theo bài ra ra có xy =70 (1)
Nếu ta bớt đi 2 dãy ghế thì mỗi dãy ghế còn lại phải xếp thêm 4 người ngồi mới đủ chỗ
=> (x-2)(y+4) = 70 (2)
Từ (1) và (2) ta có hệ phương trình...................
Giải ra được x = 7 ; y = 10

Gọi số dãy ghế có trong phòng họp lúc đầu là x (x<50)
Lúc đầu mỗi dãy có ghế
Vì lúc sau có 315 người tham dự nên phải kê thêm 3 dãy, mỗi dãy thêm 1 ghế
=>
=> x1= 60 (Loại), x2=12 (thỏa mãn)
Vậy trong phòng họp lúc đầu có 12 dãy ghế.