1. Cho hình bình hành ABCD. Đường thẳng qua C vuông góc với CD cắt đường thẳng qua A vuông góc với BD tại F. Đường thẳng qua B vuông góc với AB cắt đường trung trực của AC tại E. Hai đường thẳng BC và EF cắt nhau tại K. Tính tỉ số \(\frac{KE}{KF}\)
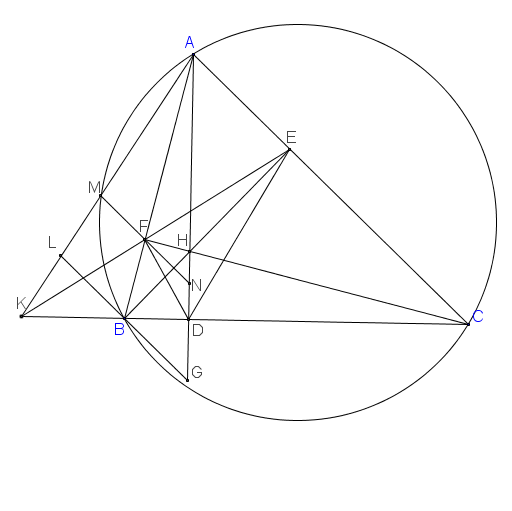
2. Cho tam giác ABC có 3 góc nhọn nội tiếp (O). M trung điểm BC, N đối xứng với M qua O. Đường thẳng qua A vuông góc với AN cắt đường thẳng qua B vuông góc với BC tại D. Kẻ đường kính AE. CMR:
a) BA.BC = 2BD.BE
b) CD đi qua trung điểm của đường cao AH của ttam giác ABC.
3. Có 10 vận động viên tham gia đấu quần vợt. Cứ 2 người trong họ chơi với nhau đúng 1 trận. Người thứ nhất thắng x1 trận và thua y1 trận; người thứ hai thắng x2 trận và thua y2 trận; ...; người thứ mười thắng x10 trận và thua y10 trận. Biết trong 1 trận đấu quần vợt ko có kết quả hòa. CMR: \(x_1^2+x_2^2+...+x_{10}^2=y_1^2+y_2^2+...+y_{10}^2\)

Chỉ hướng dẫn câu đại thôi nhé
Theo đề bài thì ta có hai giả thuyết sau
\(\hept{\begin{cases}x_1+y_1=x_2+y_2=...=x_{10}+y_{10}=10\\x_1+x_2+...+x_{10}=y_1+y_2+...+y_{10}\end{cases}}\)
Theo đề bài thì
\(x^2_1+x^2_2+...+x^2_{10}=y_1^2+y^2_2+...+y^2_{10}\)
\(\Leftrightarrow\left(x^2_1-y^2_1\right)+\left(x^2_2-y^2_2\right)+...+\left(x^2_{10}-y^2_{10}\right)=0\)
\(\Leftrightarrow10\left(x_1-y_1\right)+10\left(x_2-y_2\right)+...+\left(x_{10}-y_{10}\right)=0\)
\(\Leftrightarrow x_1+x_2+...+x_{10}-y_1-y_2-...-y_{10}=0\)ĐPCM