Cho tứ giác ABCD gọi góc nhọn tạo bởi 2 đường chéo là α, diện tích của tứ giác là S. CMR: . \(S=\frac{1}{2}.AC.BD.\sin\alpha\)Từ đó suy ra diện tích của tứ giác có hai đường chéo vuông góc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 9 2015
Làm như sau :
Kẻ AH vg BD ; CK vg BD
Sabd = 1/2.AH.BD (1)
Sbcd = 1/2.CK.BD (2)
từ (1) và (2) => Sabcd= Sabd + Sbcd = 1/2BD ( AH+CK) (*)
Tam giác AHO vuông tại H , theo tỉ số lượng giác giữa cạnh và góc
=> AH = OA . sin AOH (3)
Tương tự CK = OC.sin BOC (4)
Mà BOC = AOH => sin BOC = sin AOH (5)
Từ (3) và (4) và (5) => AH + CK = sin AOH ( OA + OC ) = AC .sin AOH (**)
Từ (*) và (**) => cái cần phải CM
XO
16 tháng 1 2022
Có hình vẽ :
Dễ thấy SABCD = \(\frac{1}{2}\left(AH+CK\right).BD\)
mà lại có \(AH=AO.sin\alpha\) ; \(CK=OC.sin\alpha\)
=> SABCD = \(\frac{1}{2}\sin\alpha.AC.BD\)
Khi 2 đường chéo vuông góc với nhau thì
\(H\equiv O\equiv K\Rightarrow AH=AO=CK\)
hay \(sin\alpha=1\)
Khi đó \(S_{ABCD}=\frac{1}{2}mn\)(đpcm)
25 tháng 9 2023
Tham khảo:
Gọi O là giao điểm của AC và BD.
a) Áp dụng công thức \(S = \frac{1}{2}ac.\sin B\), ta có:
\(\begin{array}{l}{S_{OAD}} = \frac{1}{2}.OA.OD.\sin \alpha ;\quad {S_{OBC}} = \frac{1}{2}.OB.OC.\sin \alpha ;\\{S_{OAB}} = \frac{1}{2}.OA.OB.\sin ({180^o} - \alpha );\quad {S_{OCD}} = \frac{1}{2}.OD.OC.\sin ({180^o} - \alpha ).\end{array}\)
Mà \(\sin ({180^o} - \alpha ) = \sin \alpha \)
\( \Rightarrow {S_{OAB}} = \frac{1}{2}.OA.OB.\sin \alpha ;\quad {S_{OCD}} = \frac{1}{2}.OD.OC.\sin \alpha .\)
\(\begin{array}{l} \Rightarrow {S_{ABCD}} = \left( {{S_{OAD}} + {S_{OAB}}} \right) + \left( {{S_{OBC}} + {S_{OCD}}} \right)\\ = \frac{1}{2}.OA.\sin \alpha .(OD + OB) + \frac{1}{2}.OC.\sin \alpha .(OB + OD)\\ = \frac{1}{2}.OA.\sin \alpha .BD + \frac{1}{2}.OC.\sin \alpha .BD\\ = \frac{1}{2}.BD.\sin \alpha .(OA + OC)\\ = \frac{1}{2}.AC.BD.\sin \alpha = \frac{1}{2}.x.y.\sin \alpha .\end{array}\)
b) Nếu \(AC \bot BD\) thì \(\alpha = {90^o} \Rightarrow \sin \alpha = 1.\)
\( \Rightarrow {S_{ABCD}} = \frac{1}{2}.x.y.1 = \frac{1}{2}.x.y.\)
CM
26 tháng 6 2017
a, Giả sử tam giác ABC có A ^ < 90 0 kẻ đường cáo BH. Ta có BH=AB.sin A ^
=> S ∆ A B C = 1 2 A C . B H = 1 2 A B . A C . sin A
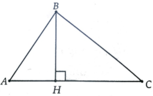
b, Giả sử tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O có
A
O
B
^
=
α
<
90
0
. Kẻ AH
⊥
BD, tại H và CK
⊥
BD tại K
Ta có: AH = OA.sinα
=> S A B D = 1 2 B D . A H = 1 2 B D . O A . sin α
Tương tự: S C B D = 1 2 B D . C K = 1 2 B D . O C . sin α
=> S A B C D = S A B D + S C B D = 1 2 B D . O A . sin α + 1 2 B D . O C . sin α = 1 2 B D . A C . sin α
TP
0
CM
9 tháng 3 2018
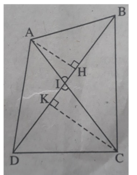
Giả sử hai đường chéo AC, BD cắt nhau tại I, ∠ (AIB) = α là góc nhọn (xem h.bs.9)
Kẻ đường cao AH của tam giác ABD và đường cao CK của tam giác CBD.
Ta có: AH = AI.sin α , CK = CI.sin α
Diện tích tam giác ABD là S A B D = 1/2 BD.AH.
Diện tích tam giác CBD là S C B D = 1/2 BD.CK.
Từ đó diện tích S của tứ giác ABCD là:
S = S A B D + S C B D = 1/2BD.(AH + CK)
= 1/2 BD.(AI + CI)sin α = 1/2BD.AC.sin α
CM
12 tháng 12 2018
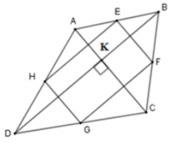
Vì E, F, G, H lần lượt là trung điểm các cạnh AB,BC,CD,DA nên EF, FG, GH, HE lần lượt là đường trung bình của tam giác ABC, BCD, ADC, ADB nên
EF//HG (cùng song song với AC)
HE//FG (cùng song song với BD)
Suy ra tứ giác EFGH là hình bình hành
Mà A C ⊥ B D (gt) ⇒ E F ⊥ F G
Suy ra EFGH là hình chữ nhật
Do đó S E F G H = H E . E F mà E F = 1 2 A C ; H E = 1 2 B D (tính chất đường trung bình)
CM
17 tháng 3 2017
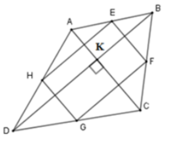
Vì E, F, G, H lần lượt là trung điểm các cạnh AB,BC,CD,DA nên EF, FG, GH, HE lần lượt là đường trung bình của tam giác ABC, BCD, ADC, ADB nên
EF//HG (cùng song song với AC)
HE//FG (cùng song song với BD)
Suy ra tứ giác EFGH là hình bình hành
Mà A C ⊥ B D (gt) ⇒ E F ⊥ F G
Suy ra EFGH là hình chữ nhật
Do đó S E F G H = H E . E F mà E F = 1 2 A C ; H E = 1 2 B D (tính chất đường trung bình)
Đáp án D